题目内容
16.在△ABC中,已知AB=AC,BC=2,点P在边BC上,若$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\frac{1}{4}$,则$\overrightarrow{PB}$•$\overrightarrow{PC}$=$-\frac{3}{4}$.分析 由题意建立平面直角坐标系,得到B,C的坐标,再设出P,A的坐标,由$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\frac{1}{4}$求得P的横坐标,代入$\overrightarrow{PB}$•$\overrightarrow{PC}$得答案.
解答 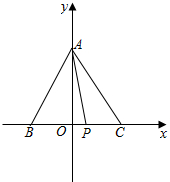 解:如图,
解:如图,
以BC所在直线为x轴,以BC的垂直平分线为y轴,建立平面直角坐标系,
则C(1,0),B(-1,0),
设A(0,n),P(m,0),则$\overrightarrow{PA}=(-m,n),\overrightarrow{PC}=(1-m,0)$,$\overrightarrow{PB}=(-1-m,0)$.
由$\overrightarrow{PA}$•$\overrightarrow{PC}$=-$\frac{1}{4}$,得-m(1-m)=-$\frac{1}{4}$,解得:$m=\frac{1}{2}$.
∴${m}^{2}-1=\frac{1}{4}-1=-\frac{3}{4}$.
故答案为:-$\frac{3}{4}$.
点评 本题考查平面向量的数量积运算,训练了利用坐标法求数量积,是中档题.

练习册系列答案
相关题目
6.下列有关命题的说法错误的是( )
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “x=1”是“x≥1”的充分不必要条件 | |
| C. | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” | |
| D. | 若命题p:?x0∈R,x02≥0,则命题¬p:?x∈R,x2<0 |
1.抛物线y2=8x上到其焦点F距离为4的点有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.直线y=-2x+b一定通过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
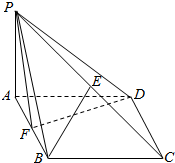 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=45°,AB=2,AD=$\sqrt{2}$,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=45°,AB=2,AD=$\sqrt{2}$,PA⊥平面ABCD,E是PC的中点,F是AB的中点.