题目内容
已知|
|=1，|
|=2且（
+
）与
垂直，则
与
的夹角是（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、135° | D、120° |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得 （
+
）•
=
2+
•
=0，求得cos＜
，
＞的值，可得＜
，
＞的值．
| a |
| b |
| a |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：由题意可得 （
+
）•
=
2+
•
=1+1×2×cos＜
，
＞=0，
求得cos＜
，
＞=-
，∴＜
，
＞=120°，
故选：D．
| a |
| b |
| a |
| a |
| a |
| b |
| a |
| b |
求得cos＜
| a |
| b |
| 1 |
| 2 |
| a |
| b |
故选：D．
点评：本题主要考查两个向量垂直的性质，两个向量的数量积的定义，属于中档题．
练习册系列答案
相关题目
长方体ABCD-A1B1C1D1，AB=2，AD=2，AA1=
，则点D到平面ACD1的距离是（ ）
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知函数f（x）=cos
，根据下列框图，输出S的值为（ ）
| πx |
| 3 |
| A、670 | ||
B、670
| ||
| C、671 | ||
| D、672 |
定义在R上的偶函数f（x）满足f（x+1）f（x）=-2（f（x）≠0），且在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（ ）
| A、f（sinα）＜f（cosβ） |
| B、f（sinα）＞f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、以上情况均有可能 |
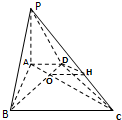如图示，在底面为直角梯形的四棱椎P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4，AD=2，AB=2