题目内容
函数f(x)=sin2x-
(cos2x-sin2x)的图象为C,如下结论中正确的是 .
①图象C关于直线x=
π对称;
②图象C关于点(
,0)对称;
③函数f(x)在区间(-
,
)内是增函数;④由y=2sin2x的图角向右平移
个单位长度可以得到图象C.
| 3 |
①图象C关于直线x=
| 11 |
| 12 |
②图象C关于点(
| 2π |
| 3 |
③函数f(x)在区间(-
| π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,命题的真假判断与应用
专题:三角函数的图像与性质
分析:先利用倍角公式、两角和差的正弦公式化简函数f(x)=sin2x-
(cos2x-sin2x)=2sin(2x-
).再利用三角函数的图象与性质进行判断即可.
| 3 |
| π |
| 3 |
解答:
解:函数f(x)=sin2x-
(cos2x-sin2x)=sin2x-
cos2x=2sin(2x-
).
①∵f(
)=2sin(2×
-
)=-2,因此图象C关于直线x=
π对称,正确;
②∵f(
)=2sin(
-
)=0,因此图象C关于点(
,0)对称,正确;
③由x∈(-
,
),得到(2x-
)∈(-
,
),因此函数f(x)在区间(-
,
)内是增函数,正确;
④由y=2sin2x的图角向右平移
个单位长度得到图象y=2sin2(x-
)=2sin(2x-
)≠2sin(2x-
),因此不正确.
综上可知:只有①②③正确.
故答案为:①②③.
| 3 |
| 3 |
| π |
| 3 |
①∵f(
| 11π |
| 12 |
| 11π |
| 12 |
| π |
| 3 |
| 11 |
| 12 |
②∵f(
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
③由x∈(-
| π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
④由y=2sin2x的图角向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
综上可知:只有①②③正确.
故答案为:①②③.
点评:本题考查了三角函数的图象与性质、倍角公式、两角和差的正弦公式、平移变换等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
对于每个非零自然数n,抛物线y=x2-
x+
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2014B2014的值是( )
| 2n+1 |
| n2+n |
| 1 |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b∈R且a≠b,若aea=beb(e为自然对数的底数),则下列正确的是( )
| A、lna-lnb=b-a |
| B、lna-lnb=a-b |
| C、ln(-a)-ln(-b)=b-a |
| D、ln(-a)-ln(-b)=a-b |
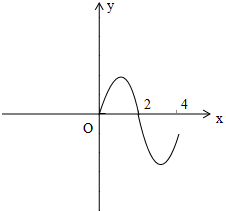 已知奇函数f(x)的定义域为[-4,4],且当x∈[0,4]时,f(x)的函数图象如图所示,解不等式:
已知奇函数f(x)的定义域为[-4,4],且当x∈[0,4]时,f(x)的函数图象如图所示,解不等式:
 正四面体ABCD边长为2.E,F分别为AC,BD中点.
正四面体ABCD边长为2.E,F分别为AC,BD中点.