题目内容
13.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,且右焦点到一条渐近线的距离为$\sqrt{3}$,双曲线的方程为( )| A. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{3}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
分析 根据题意,由双曲线的离心率公式可得e=$\frac{c}{a}$=2,即c=2a,又由双曲线的性质可得b=$\sqrt{3}$,结合c2=a2+b2,计算可得a2的值,将a2、b2的值代入双曲线方程即可得答案.
解答 解:根据题意,双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,
则e=$\frac{c}{a}$=2,即c=2a,
又由右焦点到一条渐近线的距离为$\sqrt{3}$,则有b=$\sqrt{3}$,
又由c2=a2+b2,即4a2=a2+3,
则有a2=1,
则双曲线的方程为:x2-$\frac{{y}^{2}}{3}$=1;
故选:B.
点评 本题考查双曲线的几何性质,注意双曲线中焦点到渐近线的距离为b.

练习册系列答案
相关题目
1.(x2-1)($\frac{1}{x}$-2)5的展开式的常数项为( )
| A. | 112 | B. | 48 | C. | -112 | D. | -48 |
8.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{9}x,x>0}\\{{4}^{-x}+\frac{3}{2},x≤0}\end{array}\right.$,则f(27)+f(-log43)的值为( )
| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
18.已知全集U=R,集合A={x|x(x-2)<0},B={x||x|≤1},则下列阴影部分表示的集合是( )

| A. | (0,1] | B. | (-2,-1)∪[0,1] | C. | [-1,0]∪(1,2) | D. | [-1,2) |
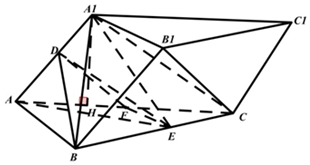 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.