题目内容
4.与向量$\overrightarrow a=({4,3})$方向相反的单位向量是$({-\frac{4}{5},-\frac{3}{5}})$.分析 与向量$\overrightarrow a=({4,3})$方向相反的单位向量是-$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$.
解答 解:与向量$\overrightarrow a=({4,3})$方向相反的单位向量是:
-$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$=-$\frac{(4,3)}{\sqrt{16+9}}$=(-$\frac{4}{5}$,-$\frac{3}{5}$).
故答案为:(-$\frac{4}{5}$,-$\frac{3}{5}$).
点评 本题考查与已知向量方向相反的单位向量的求法,涉及到平面向量坐标运算法则等基础知识,考查运算求解能力,考查化归与转化思想,是基础题.

练习册系列答案
相关题目
15.函数f(x)=(1-cos2x)cos2x,x∈R,设f(x)的最大值是A,最小正周期为T,则f(AT)的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
12.已知集合A={x|y=$\sqrt{x+1}$},B={y=|y=1-ex},则A∩B=( )
| A. | [-1,1) | B. | [-1,1] | C. | (-1,1) | D. | (-∞,-1]∪[1,+∞) |
13.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,且右焦点到一条渐近线的距离为$\sqrt{3}$,双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{3}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
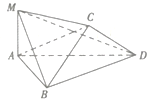 如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$
如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$