题目内容
10.以下四个命题:①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为$\frac{1+a}{2}$;
②设a、b∈R,则“log2a>log2b”是“2a-b>1”的充分不必要条件;
③函数f(x)=${x}^{\frac{1}{2}}$-($\frac{1}{2}$)x的零点个数为1;
④命题p:?n∈N,3n≥n2+1,则¬p为?n∈N,3n≤n2+1.
其中真命题的序号为②③.
分析 由曲线关于y轴对称,由概率分布特点,即可判断①;运用对数函数和指数函数的单调性,结合充分必要条件的定义,即可判断②;画出y=${x}^{\frac{1}{2}}$和y=($\frac{1}{2}$)x的图象,即可判断③;由全称命题的否定为特称命题,即可判断④.
解答 解:①已知随机变量X~N(0,σ2),若P(|X|<2)=a,
则P(X>2)=$\frac{1}{2}$(1-P(|X|<2))=$\frac{1-a}{2}$,故①错;
②设a、b∈R,log2a>log2b?a>b>0⇒a-b>0⇒2a-b>1,由于a-b>0,a,b不一定大于0,
则“log2a>log2b”是“2a-b>1”的充分不必要条件,故②对;
③由y=${x}^{\frac{1}{2}}$和y=($\frac{1}{2}$)x的图象,可得它们只有一个交点,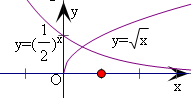
即函数f(x)=${x}^{\frac{1}{2}}$-($\frac{1}{2}$)x的零点个数为1,故③对;
④命题p:?n∈N,3n≥n2+1,则¬p为?n∈N,3n<n2+1.故④错.
故答案为:②③.
点评 本题考查命题的真假判断,主要是正态分布的特点和充分必要条件的判断、及函数的零点个数和命题的否定,考查判断能力和数形结合思想,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
13.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,且右焦点到一条渐近线的距离为$\sqrt{3}$,双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{3}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
18.若由曲线y=x2+k2与直线y=2kx及y轴所围成的平面图形的面积S=9,则k=( )
| A. | 3$\sqrt{3}$ | B. | -3或3 | C. | 3 | D. | -3 |
15.为了判断高中学生的文理科选修是否与性别有关系,随机调查了50名学生,得到如下2×2的列联表:
附:
根据表中数据,得到${x^2}=\frac{{50×{{({13×20-10×7})}^2}}}{23×27×20×30}≈4.844$,则认为选修文理科与性别有关系的可能性不低于95%.
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
19.已知集合A={x|$\frac{3x-4}{2-x}$≥0},B={x|x2-2x<0},则A∩B=( )
| A. | [$\frac{4}{3}$,2) | B. | [$\frac{3}{4}$,2] | C. | ($\frac{3}{4}$,2) | D. | (-$∞,\frac{3}{4}$)∪(2,+∞) |
20.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为$\frac{1}{2}$,则a的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
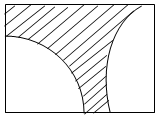 已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.
已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.