题目内容
1.(x2-1)($\frac{1}{x}$-2)5的展开式的常数项为( )| A. | 112 | B. | 48 | C. | -112 | D. | -48 |
分析 利用通项公式即可得出.
解答 解:($\frac{1}{x}$-2)5的展开式的通项公式为:Tr+1=${∁}_{5}^{r}$(-2)5-r$(\frac{1}{x})^{r}$=${∁}_{5}^{r}$(-2)5-rx-r.
令-r=-2,-r=0,分别解得r=2,r=0.
∴(x2-1)($\frac{1}{x}$-2)5的展开式的常数项=$1×{∁}_{5}^{2}(-2)^{3}$-1×1×(-2)5=-48.
故选:D.
点评 本题考查了二项式定理的应用、方程思想方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知集合A={x|y=$\sqrt{x+1}$},B={y=|y=1-ex},则A∩B=( )
| A. | [-1,1) | B. | [-1,1] | C. | (-1,1) | D. | (-∞,-1]∪[1,+∞) |
13.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,且右焦点到一条渐近线的距离为$\sqrt{3}$,双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{3}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
18.若由曲线y=x2+k2与直线y=2kx及y轴所围成的平面图形的面积S=9,则k=( )
| A. | 3$\sqrt{3}$ | B. | -3或3 | C. | 3 | D. | -3 |
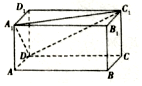 在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.
在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.