题目内容
5.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2}-1(x<1)}\\{\frac{lnx}{x}(x≥1)}\end{array}}\right.$关于x的方程2[f(x)]2+(1-2m)f(x)-m=0,有5不同的实数解,则m的取值范围是( )| A. | $(-1,\frac{1}{e})$ | B. | (0,+∞) | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{e}]$ |
分析 利用导数研究函数y=$\frac{lnx}{x}$的单调性并求得最值,求解方程2[f(x)]2+(1-2m)f(x)-m=0得到f(x)=m或f(x)=$-\frac{1}{2}$.画出函数图象,数形结合得答案.
解答 解:设y=$\frac{lnx}{x}$,则y′=$\frac{1-lnx}{{x}^{2}}$,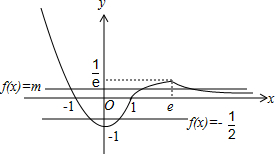
由y′=0,解得x=e,
当x∈(0,e)时,y′>0,函数为增函数,当x∈(e,+∞)时,y′<0,函数为减函数.
∴当x=e时,函数取得极大值也是最大值为f(e)=$\frac{1}{e}$.
方程2[f(x)]2+(1-2m)f(x)-m=0化为[f(x)-m][2f(x)+1]=0.
解得f(x)=m或f(x)=$-\frac{1}{2}$.
如图画出函数图象:
可得m的取值范围是(0,$\frac{1}{e}$).
故选:C.
点评 本题考查根的存在性与根的个数判断,考查利用导数求函数的最值,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知集合A={x|3x<16,x∈N},B={x|x2-5x+4<0},则A∩(∁RB)=( )
| A. | {1,2} | B. | {0,1} | C. | {0,1,2} | D. | {x|0<x<1} |
13.给出以下结论:
(1)直线a∥平面α,直线b?α,则a∥b.
(2)若a?α,b?α,则a、b无公点.
(3)若a?α,则a∥α或a与α相交
(4)若a∩α=A,则a?α.
正确的个数为( )
(1)直线a∥平面α,直线b?α,则a∥b.
(2)若a?α,b?α,则a、b无公点.
(3)若a?α,则a∥α或a与α相交
(4)若a∩α=A,则a?α.
正确的个数为( )
| A. | 1个 | B. | 4个 | C. | 3个 | D. | 2个 |
17.已知函数f(x)=$\frac{1}{3}{x^3}$-x+c+1有两个不同零点,且有一个零点恰为f(x)的极小值点,则c的值为( )
| A. | 0 | B. | $-\frac{5}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{5}{3}$或$-\frac{1}{3}$ |
14.已知ω>0,函数f(x)=sinωx在区间$[{-\frac{π}{4},\frac{π}{4}}]$上恰有9个零点,则ω的取值范围是( )
| A. | 16≤ω<20 | B. | 16≤ω≤20 | C. | 16≤ω<18 | D. | 16≤ω≤18 |
15.△ABC中,a,b,c分别为角A,B,C的对边,a=$\sqrt{3}$,b=$\sqrt{2}$,B=45°,则角C的大小为( )
| A. | 15° | B. | 75° | C. | 15°或75° | D. | 60°或120° |
 为了了解某校学生一学期内的课外阅读情况,现随机统计了n名学生的课外阅读时间,所得样本数据都在[50,150]内(单位:小时),其频率分布直方图如图所示,若该样本在[125,150]内的频数为100,则n的值为500.
为了了解某校学生一学期内的课外阅读情况,现随机统计了n名学生的课外阅读时间,所得样本数据都在[50,150]内(单位:小时),其频率分布直方图如图所示,若该样本在[125,150]内的频数为100,则n的值为500.