题目内容
10.已知函数f(x)=ax2-(a+2)x+lnx.若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,则a的取值范围为[0,8].分析 由题意设g(x)=f(x)+2x,(x>0),g(x)是增函数,即g'(x)≥0在(0,+∞)上恒成立,求出a的取值范围.
解答 解:令g(x)=f(x)+2x=ax2-ax+lnx,(x>0);
由题意知g(x)在(0,+∞)单调递增,
所以g'(x)=2ax-a+$\frac{1}{x}$≥0在(0,+∞)上恒成立,
即2ax2-ax+1≥0在(0,+∞)上恒成立;
令h(x)=2ax2-ax+1,(x>0);
则①若a=0,h(x)=1≥0恒成立,
②若a<0,二次函数h(x)≥0不恒成立,舍去
③若a>0,二次函数h(x)≥0恒成立,
只需满足最小值h($\frac{1}{4}$)≥0,
即$\frac{a}{8}$-$\frac{a}{4}$+1≥0,解得0<a≤8;
综上,a的取值范围是[0,8].
故答案为:[0,8].
点评 本题考查了应用导数判定函数的增减性和恒成立问题的解法,是中档题.

练习册系列答案
相关题目
1.设f(x)可导且下列各极限均存在,则( )成立.
| A. | $\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x}$=f′(0) | B. | $\underset{lim}{h→0}$$\frac{f(a+2h)-f(a)}{h}$=f′(a) | ||
| C. | $\underset{lim}{△x→0}$$\frac{f({x}_{0})-f({x}_{0}-△x)}{△x}$=f′(x0) | D. | $\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0}-△x)}{2△x}$=f′(x0) |
5.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2}-1(x<1)}\\{\frac{lnx}{x}(x≥1)}\end{array}}\right.$关于x的方程2[f(x)]2+(1-2m)f(x)-m=0,有5不同的实数解,则m的取值范围是( )
| A. | $(-1,\frac{1}{e})$ | B. | (0,+∞) | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{e}]$ |
19.某市5年中的煤气消耗量与使用煤气户数的历史资料如下:
(1)检验是否线性相关;
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
( $b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)\;({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}a=\overline y-b\overline x$)
| 年份 | 2006 | 2007 | 2008 | 2009 | 2010 |
| x用户(万户) | 1 | 1.1 | 1.5 | 1.6 | 1.8 |
| y(万立方米) | 6 | 7 | 9 | 11 | 12 |
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
( $b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)\;({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}a=\overline y-b\overline x$)
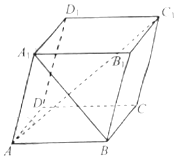 已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.
已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.