题目内容
7.已知函数f(x)的定义域为R,且为可导函数,若对?x∈R,总有2f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),则( )| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
分析 令g(x)=x2f(x),求出函数的导数,得到函数g(x)的单调区间,从而求出函数的最大值,求出答案即可.
解答 解:令g(x)=x2f(x),
则g′(x)=x[2f(x)+xf′(x)],
若对?x∈R,总有2f(x)+xf′(x)<0成立
则x>0时,g′(x)<0,x<0时,g′(x)>0,
故g(x)在(-∞,0)递增,在(0,+∞)递减,
故g(x)max=g(0)=0,
故选:C.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,设出g(x)是解题的关键,本题是一道基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.直三棱柱A1B1C1-ABC,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{30}}}{10}$ | C. | $\frac{{\sqrt{30}}}{15}$ | D. | $\frac{{\sqrt{15}}}{10}$ |
19.双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的焦点到渐近线的距离为( )
| A. | $2\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
16.在三棱锥P-ABC中,PA⊥平面ABC,PA=2$\sqrt{3}$,BC=2,则三棱锥P-ABC的外接球的表面积的最小值为( )
| A. | 13π | B. | 14π | C. | 15π | D. | 16π |
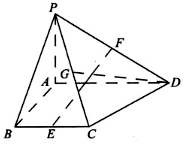 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点. 若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.
若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.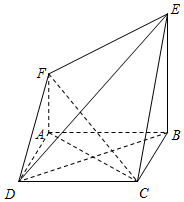 如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.