题目内容
如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE=PA，∠ABC=60°，PD=1，BD=8，则BC= ．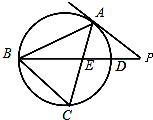
考点：与圆有关的比例线段
专题：推理和证明,立体几何
分析：由PD=1，BD=8我们不难求出割线PB被圆截得的两条线段的长，根据切割线定理，我们进而可以求出切线PA的长度，由PE=PA及弦切角定理，我们可以得到△AEP为等边三角形，结合余弦定理，可以求出AD的长，根据相似三角性质，即可求出BC的长．
解答：
解：∵PB=PD+BD=1+8=9，
由切割线定理得：PA2=PD•BD=9，
∴PA=3，
由弦切角定理得：∠PAC=∠ABC=60°，又由PA=PE
∴△PAE为等边三角形，则AE=PA=3，
连接AD，在△ADE中，ED=PE-PD=2，
由余弦定理得：AD=
，
又△AED～△BEC，相似比=ED：BE=1：2，
∴BC=2
．
故答案为：2
．
解：∵PB=PD+BD=1+8=9，由切割线定理得：PA2=PD•BD=9，
∴PA=3，
由弦切角定理得：∠PAC=∠ABC=60°，又由PA=PE
∴△PAE为等边三角形，则AE=PA=3，
连接AD，在△ADE中，ED=PE-PD=2，
由余弦定理得：AD=
| 7 |
又△AED～△BEC，相似比=ED：BE=1：2，
∴BC=2
| 7 |
故答案为：2
| 7 |
点评：本题是考查同学们推理能力、逻辑思维能力的好资料，题目以证明题为主，特别是一些定理的证明和用多个定理证明一个问题的题目，我们注意熟练掌握：1．射影定理的内容及其证明； 2．圆周角与弦切角定理的内容及其证明；3．圆幂定理的内容及其证明；4．圆内接四边形的性质与判定．
练习册系列答案
相关题目
已知集合A={x|0＜log4x＜1}，B={x|x≤3}，则A∩B=（ ）
| A、（0，1） |
| B、（0，3] |
| C、（1，3） |
| D、（1，3] |
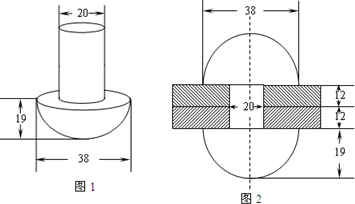如图，在两块钢板上打孔，用顶帽呈半球形，钉身为圆柱形的铆钉（图1）穿在一起，在没有帽的一段每打出一个帽，使得与顶帽的大小相等，铆合的两块钢板，成为某种钢结构的配件，其截面图如图2（单位：mm）（加工中不计损失）．