题目内容
设
=(x,-1),
=(2,3)若
与
的关系为钝角,求x的取值范围.
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:
与
的夹角为钝角,
•
<0,且与不能反向共线,解出即可.
| a |
| b |
| a |
| b |
解答:
解:当
∥
时,3x=-2,解得x=-
∵
与
的夹角为钝角,
∴
•
<0,
∴2x-3<0,
解得x<
,且x≠-
.
∴x的取值范围为(-∞,-
)∪(-
,
)
| a |
| b |
| 2 |
| 3 |
∵
| a |
| b |
∴
| a |
| b |
∴2x-3<0,
解得x<
| 3 |
| 2 |
| 2 |
| 3 |
∴x的取值范围为(-∞,-
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查了数量积的关系、向量的夹角公式、向量共线定理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=log2(x+
)(x∈R)的奇偶性为( )
| x2+1 |
| A、偶函数 |
| B、奇函数 |
| C、非奇非偶函数 |
| D、既是奇函数又是偶函数 |
下列说法正确的个数为( )
①“x>y”是“lgx>lgy”的充要条件;
②“a>b”是“ac2>bc2”的必要不充分条件;
③“k=
”是“直线y=kx+2与圆x2+y2=1相切”的充分不必要条件;
④“α>β”是“sinα>sinβ”既不充分又不必要条件.
①“x>y”是“lgx>lgy”的充要条件;
②“a>b”是“ac2>bc2”的必要不充分条件;
③“k=
| 3 |
④“α>β”是“sinα>sinβ”既不充分又不必要条件.
| A、3 个 |
| B、4 个 |
| C、1 个 |
| D、2个 |
已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和y轴的距离之和的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
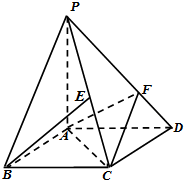 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.