题目内容
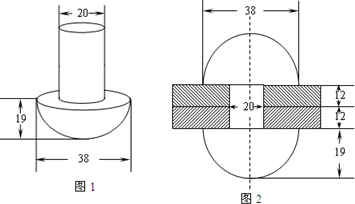 如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).
如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).(1)若钉身长度是顶帽长度的2倍,求铆钉的表面积;
(2)若每块钢板的厚底为12mm,求钉身的长度(结果精确到1mm).
考点:组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:(1)根据图象结合圆柱和球的表面积公式即可求铆钉的表面积;
(2)根据体积公式即可求钉身的长度.
(2)根据体积公式即可求钉身的长度.
解答:
解:(1)设钉身的高为h,钉身的底面半径为r,钉帽的底面半径为R,
由题意可知圆柱的高h=2R=38,圆柱的侧面积S1=2πrh=760π,
半球的表面积S2=
×4πR2+πR2=1083π,
故铆钉的表面积S=S1+S2=760π+1083π=1843π.
(2)V1=πr2h1=100×24π=2400π,V2=
×
πR3=
×193π=
,
设钉身的长度为l,则V3=πr2•l=100πl,
由于V3=V1+V2,
∴2400π+
=100πl,
解得l≈70mm.
由题意可知圆柱的高h=2R=38,圆柱的侧面积S1=2πrh=760π,
半球的表面积S2=
| 1 |
| 2 |
故铆钉的表面积S=S1+S2=760π+1083π=1843π.
(2)V1=πr2h1=100×24π=2400π,V2=
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 13718π |
| 3 |
设钉身的长度为l,则V3=πr2•l=100πl,
由于V3=V1+V2,
∴2400π+
| 13718π |
| 3 |
解得l≈70mm.
点评:本题主要考查空间几何体的体积和表面积的计算,要求熟练掌握相应的表面积和体积公式.

练习册系列答案
相关题目
为了得到y=cos4x,x∈R的图象,只需把余弦曲线上所有点的( )
| A、横坐标伸长到原来的4倍,纵坐标不变 | ||
B、横坐标伸长到原来的
| ||
| C、纵坐标伸长到原来的4倍,横坐标不变 | ||
D、纵坐标伸长到原来的
|
已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和y轴的距离之和的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知函数f(x)=
,设b>a≥0,若f(a)=f(b),则a•f(b)的取值范围是( )
|
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
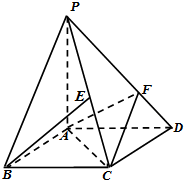 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,E为PC中点,PF=2FD,求证:BE∥平面AFC.