题目内容
1.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与圆${C_2}:{x^2}+{y^2}={c^2}$(c是双曲线的半焦距)相交于第二象限内一点M,点N在x轴下方且在圆C2上,又F1,F2分别是双曲线C1的左右焦点,若$∠{F_2}NM=\frac{π}{3}$,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
分析 由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,根据此直角三角形,结合双曲线的离心率的定义即可求得双曲线的离心率.
解答 解:由题设知圆C2的直径为F1F2,
则$∠{F_1}M{F_2}=\frac{π}{2}$,
又$∠M{F_1}{F_2}=∠{F_2}NM=\frac{π}{3}$,
所以$∠{F_1}{F_2}M=\frac{π}{6}$,所以|MF1|=c,$|{M{F_2}}|=\sqrt{3}c$,
由双曲线的定义得|MF2|-|MF1|=2a,即$(\sqrt{3}-1)c=2a$,
所以$e=\frac{2}{{\sqrt{3}-1}}=\sqrt{3}+1$,
故选C.
点评 本题考查双曲线的离心率,考查双曲线的定义的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知数列{an}是等比数列,若${a_2}=1,{a_5}=\frac{1}{8}$,则${a_1}{a_2}+{a_2}{a_3}+…+{a_n}{a_{n+1}}({n∈{N^*}})$的取值范围是( )
| A. | $({\frac{2}{3},2}]$ | B. | $[{1,\frac{8}{3}})$ | C. | $[{2,\frac{8}{3}})$ | D. | $({-∞,\frac{8}{3}})$ |
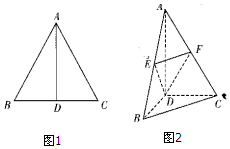 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.