题目内容
9.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=-x2+ax.(I)求函数f(x)的解析式;
(II)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
分析 (I)当x<0时,-x>0,由已知表达式可求f(-x),根据奇函数性质可求f(x);
(II)①借助二次函数图象的特征及奇函数性质可求a的范围;
②利用奇函数性质及单调递减性质可去掉不等式中的符号“f”,进而可转化为函数最值问题处理.
解答 解:(I)当x<0时,-x>0,又因为f(x)为奇函数,
所以f(x)=-f(-x)=-(-x2-ax)=x2+ax,
所以f(x)=$\left\{\begin{array}{l}{-{x}^{2}+ax,x≥0}\\{{x}^{2}+ax,x<0}\end{array}\right.$.
(II)①当a≤0时,对称轴x=$\frac{a}{2}$≤0,所以f(x)=-x2+ax在[0,+∞)上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以f(x)在(-∞,0)上单调递减,
所以a≤0时,f(x)在R上为单调递减函数,
当a>0时,f(x)在(0,$\frac{a}{2}$)递增,在($\frac{a}{2}$,+∞)上递减,不合题意,
所以函数f(x)为单调减函数时,a的范围为a≤0.
②f(m-1)+f(m2+t)<0,∴f(m-1)<-f(m2+t),
又f(x)是奇函数,∴f(m-1)<f(-t-m2),
又因为f(x)为R上的单调递减函数,所以m-1>-t-m2恒成立,
所以$t>-{m}^{2}-m+1=-(m+\frac{1}{2})^{2}+\frac{5}{4}$恒成立,所以t>$\frac{5}{4}$,
即实数t的范围为:($\frac{5}{4}$,+∞).
点评 本题考查函数的奇偶性、单调性及其应用,考查不等式恒成立问题,考查学生分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.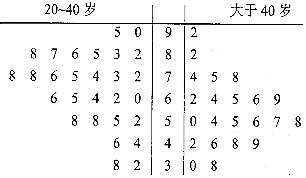 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为X,求X的分布列和数学期望.
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
14.已知实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ x-y≤2\\ 0≤x≤1\end{array}\right.$则z=2x+4y的最大值是( )
| A. | -4 | B. | 2 | C. | 6 | D. | 8 |
1.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与圆${C_2}:{x^2}+{y^2}={c^2}$(c是双曲线的半焦距)相交于第二象限内一点M,点N在x轴下方且在圆C2上,又F1,F2分别是双曲线C1的左右焦点,若$∠{F_2}NM=\frac{π}{3}$,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P(x0,$\frac{5}{2}$)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1 | D. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1 |
19.已知函数f(x)是偶函数,定义域为R,g(x)=f(x)+2x,若g(log27)=3,则$g({{{log}_2}\frac{1}{7}})$=( )
| A. | -4 | B. | 4 | C. | $-\frac{27}{7}$ | D. | $\frac{27}{7}$ |