题目内容
13.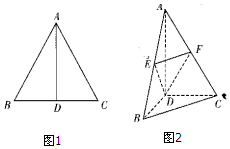 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.(1)求证:BC∥平面DEF;
(2)求多面体D-BCEF的体积.
分析 (1)推导出EF∥BC.由此能证明BC∥平面DEF.
(Ⅱ)推导出AD⊥BD,AD⊥CD,从而AD⊥平面BCD,进而得到VD-BCFE=V三棱锥A-BCD-V三棱锥F-ADE,由此能求出多面体D-BCEF的体积.
解答 证明:(1)因为点E,F分别是AB,AC的中点,所以EF∥BC.
又因为BC?平面DEF,EF?平面DEF,
所以BC∥平面DEF. …(5分)
解:(2)依题意,AD⊥BD,AD⊥CD,且BD∩DC=D,
所以AD⊥平面BCD,
又因为二面角B-AD-C为直二面角,所以BD⊥CD,
所以${V_{三棱锥A-BCD}}=\frac{1}{3}{S_{△BCD}}•AD=\frac{1}{3}×\frac{1}{2}×1×1×\sqrt{3}=\frac{{\sqrt{3}}}{6}$,
${V_{三棱锥F-ADE}}=\frac{1}{3}{S_{△ADE}}•\frac{1}{2}CD=\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\frac{1}{2}×\frac{1}{2}×1=\frac{{\sqrt{3}}}{24}$,
所以${V_{D-BCFE}}={V_{三棱锥A-BCD}}-{V_{三棱锥F-ADE}}=\frac{{\sqrt{3}}}{6}-\frac{{\sqrt{3}}}{24}=\frac{{\sqrt{3}}}{8}$. …(12分)
点评 本题考查线面平行的证明,考查多面体D-BCEF的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
16.圆心为(0,1)且与直线y=2相切的圆的方程为( )
| A. | (x-1)2+y2=1 | B. | (x+1)2+y2=1 | C. | x2+(y-1)2=1 | D. | x2+(y+1)2=1 |
1.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与圆${C_2}:{x^2}+{y^2}={c^2}$(c是双曲线的半焦距)相交于第二象限内一点M,点N在x轴下方且在圆C2上,又F1,F2分别是双曲线C1的左右焦点,若$∠{F_2}NM=\frac{π}{3}$,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P(x0,$\frac{5}{2}$)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1 | D. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1 |