题目内容
11.已知曲线C:x2=2py(p≠0)与直线x-y-1=0相切,过曲线C的准线上任一点M引曲线C的切线,切点分别为A、B.(1)求P的值;
(2)求△MAB面积的最小值.
分析 (1)曲线C:x2=2py(p≠0)与直线x-y-1=0联立,可得x2-2px+2p=0,利用△=4p2-8p=0,即可求p的值;
(2)表示出△MAB面积,换元,利用函数的单调性,即可求△MAB面积的最小值.
解答 解:(1)曲线C:x2=2py(p≠0)与直线x-y-1=0联立,可得x2-2px+2p=0
△=4p2-8p=0,∵p≠0∴p=2…(4分)
(2)设A(x1,y1),B(x2,y2),x2=4y,准线y=-1…(5分)
M(t,-1),y=$\frac{1}{4}{x}^{2}$,…(6分)
切线PA:y-y1=$\frac{1}{2}$x1(x-x1),∴y=$\frac{1}{2}$x1x-y1,
经过M(t,-1)∴-1=$\frac{1}{2}$x1t-y1,
同理可求-1=$\frac{1}{2}$x2t-y2,∴AB的方程为-1=$\frac{1}{2}$xt-y,
即y=$\frac{1}{2}$tx+1 …(8分)
代入抛物线方程可得x2-2tx-4=0,x1+x2=2t,x1•x2=-4,
∴|AB|=$\sqrt{1+\frac{1}{4}{t}^{2}}$|x1-x2|=t2+4,
M点到AB距离d=$\frac{|\frac{1}{2}{t}^{2}+2|}{\sqrt{1+\frac{1}{4}{t}^{2}}}$=$\sqrt{{t}^{2}+4}$,
△MAB面积S=$\frac{1}{2}$|AB|d=$\frac{1}{2}$$\sqrt{{t}^{2}+4}$•(t2+4),
令$\sqrt{{t}^{2}+4}$=a(a≥2),f(a)=$\frac{1}{2}{a}^{3}$在[2,+∞)上单调递增,∴f(a)≥4,
∴△MAB面积的最小值为4 …(12分)
点评 本题考查直线与抛物线的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
| A. | -4 | B. | 4 | C. | $-\frac{27}{7}$ | D. | $\frac{27}{7}$ |
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{{2\sqrt{2}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{5}$ |
| A. | -i | B. | -2i | C. | -1 | D. | -2 |
| A. | $[{-\frac{1}{4},\frac{1}{4}}]$ | B. | [0,$\frac{1}{4}$] | C. | [-2,$\frac{1}{4}$] | D. | [-1,$\frac{1}{4}$] |
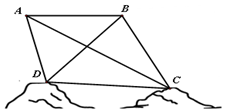 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.