题目内容
6.已知数列{an}是等比数列,若${a_2}=1,{a_5}=\frac{1}{8}$,则${a_1}{a_2}+{a_2}{a_3}+…+{a_n}{a_{n+1}}({n∈{N^*}})$的取值范围是( )| A. | $({\frac{2}{3},2}]$ | B. | $[{1,\frac{8}{3}})$ | C. | $[{2,\frac{8}{3}})$ | D. | $({-∞,\frac{8}{3}})$ |
分析 利用等比数列的通项公式与求和公式即可得出.
解答 解:由已知得数列{an}的公比满足q3=$\frac{{a}_{5}}{{a}_{2}}$=$\frac{1}{8}$,解得q=$\frac{1}{2}$,
∴a1=2,a3=$\frac{1}{2}$,
故数列{anan+1}是以2为首项,公比为$\frac{{a}_{2}{a}_{3}}{{a}_{1}{a}_{2}}$=$\frac{1}{4}$的等比数列,
∴a1a2+a2a3+…+anan+1=$\frac{2[1-(\frac{1}{4})^{n}]}{1-\frac{1}{4}}$=$\frac{8}{3}$$[1-(\frac{1}{4})^{n}]$∈$[2,\frac{8}{3})$,
故选:C.
点评 本题考查了等比数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.等比数列{an}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
17.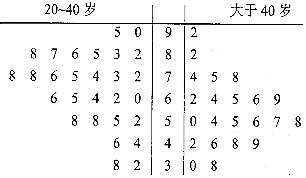 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为X,求X的分布列和数学期望.
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
14.已知实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ x-y≤2\\ 0≤x≤1\end{array}\right.$则z=2x+4y的最大值是( )
| A. | -4 | B. | 2 | C. | 6 | D. | 8 |
1.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与圆${C_2}:{x^2}+{y^2}={c^2}$(c是双曲线的半焦距)相交于第二象限内一点M,点N在x轴下方且在圆C2上,又F1,F2分别是双曲线C1的左右焦点,若$∠{F_2}NM=\frac{π}{3}$,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
11. 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P(x0,$\frac{5}{2}$)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1 | D. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1 |
16.已知$sin(θ-\frac{π}{4})=\frac{1}{5}$,则$cos(θ+\frac{π}{4})$=( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{{2\sqrt{2}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{5}$ |