题目内容
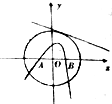 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是考点:轨迹方程,抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:焦点到A和B的距离之和等于A和B分别到准线的距离和,而距离之和为A和B的中点O到准线的距离的二倍是定值,结合椭圆的定义得焦点的轨迹方程C是以A和B为焦点的椭圆.
解答:
解:由题设知,焦点到A和B的距离之和等于A和B分别到准线的距离和.
而距离之和为A和B的中点O到准线的距离的二倍,即为2r=6,
根据椭圆的定义得,所以焦点的轨迹方程C是以A和B为焦点的椭圆,且a=3,c=2,
所以b=
=
,
所以抛物线焦点的轨迹方程是
+
=1(x≠±3).
故答案为:
+
=1(x≠±3).
而距离之和为A和B的中点O到准线的距离的二倍,即为2r=6,
根据椭圆的定义得,所以焦点的轨迹方程C是以A和B为焦点的椭圆,且a=3,c=2,
所以b=
| a2-c2 |
| 5 |
所以抛物线焦点的轨迹方程是
| x2 |
| 9 |
| y2 |
| 5 |
故答案为:
| x2 |
| 9 |
| y2 |
| 5 |
点评:本小题主要考查椭圆的定义、圆锥曲线的轨迹问题等基础知识,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知复数z=3+4i,
表示复数z的共轭复数,则复数
在付平面内对应的点在( )
. |
| z |
| ||
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |