题目内容
设常数a∈R.若(x2+
)5的二项展开式中x7项的系数为-15,则a= .
| a |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为7求出含x7的系数,列出方程解得a.
解答:
解:(x2+
)5展开式的通项为 Tr+1=
(x2)5-r(
)r=ar
x10-3r,
令 10-3r=7得r=1,
故展开式中x7项的系数为aC51=-15,解得a=-3,
故答案为:-3.
| a |
| x |
| C | r 5 |
| a |
| x |
| C | r 5 |
令 10-3r=7得r=1,
故展开式中x7项的系数为aC51=-15,解得a=-3,
故答案为:-3.
点评:本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具,属于中档题.

练习册系列答案
相关题目
若(x-
)8展开式中含x2的项的系数为7,则a=( )
| 1 |
| ax |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
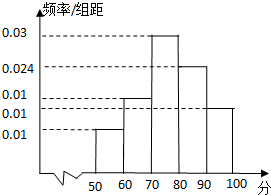 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.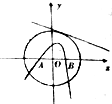 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是