题目内容
近期人们都在关注马航MH370事件,某机构通过问卷的方式,调查我市市民获取MH370事件消息的浇,得到如下数据:
按消息来源分层抽样50人,其中属于看电视的占27人.
(Ⅰ)求m的值;
(Ⅱ)从“其它渠道”中按性别比例抽取一个容量为6的样本,再从这6人中抽取3人,求至少人是女性的概率;
(Ⅲ)现从(Ⅱ)中确定的样本中每次都抽取一人,直到抽出所有女性为止,设所要抽取的人为x,求x的分布列和期望.
| 获取消息渠道 | 看电视 | 收听广播 | 其它渠道 |
| 男性 | 480 | m | 180 |
| 女性 | 384 | 210 | 90 |
(Ⅰ)求m的值;
(Ⅱ)从“其它渠道”中按性别比例抽取一个容量为6的样本,再从这6人中抽取3人,求至少人是女性的概率;
(Ⅲ)现从(Ⅱ)中确定的样本中每次都抽取一人,直到抽出所有女性为止,设所要抽取的人为x,求x的分布列和期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(Ⅰ)按照分层抽样50人,其中属于看电视的占27人,可求m的值;
(Ⅱ)个容量为6的样本,男性抽取人数4人,女性抽取人数为2人,利用对立事件的概率公式,即可求至少人是女性的概率;
(Ⅲ)由题可知:X可能取值为2,3,4,5,6,分别求出相对应的概率,由此能求出x的分布列和期望.
(Ⅱ)个容量为6的样本,男性抽取人数4人,女性抽取人数为2人,利用对立事件的概率公式,即可求至少人是女性的概率;
(Ⅲ)由题可知:X可能取值为2,3,4,5,6,分别求出相对应的概率,由此能求出x的分布列和期望.
解答:
解:(Ⅰ)由题意,
=
,解得:m=256…(2分)
(Ⅱ)“其它渠道”中,男性抽取人数
×180=4(人),女性抽取人数为6-4=2(人)
设“至少有一份是女性”为事件A
则P(A)=1-
=
…(6分)
(Ⅲ)由题可知:X可能取值为2,3,4,5,6
而P(x=2)=
=
,P(X=3)=
=
P(X=4)=
=
,P(X=5)=
,P(X=6)=
…(10分)
因此分布列
∴E(X)=
…(12分)
| 27 |
| 50 |
| 480+384 |
| 480+384+210+180+90+m |
(Ⅱ)“其它渠道”中,男性抽取人数
| 6 |
| 180+90 |
设“至少有一份是女性”为事件A
则P(A)=1-
| ||
|
| 4 |
| 5 |
(Ⅲ)由题可知:X可能取值为2,3,4,5,6
而P(x=2)=
| ||
|
| 1 |
| 15 |
| ||||||
|
| 2 |
| 15 |
| ||||||
|
| 1 |
| 5 |
| 4 |
| 15 |
| 1 |
| 3 |
因此分布列
| X | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| 14 |
| 3 |
点评:本题考查离散型随机变量的分布列和数学期望,考查分层抽样,考查概率的计算,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=-
x3+2ax2+3x(a>0)的导数f′(x)的最大值为5,则在函数f(x)图象上的点(1,f(1))处的切线方程是( )
| 2 |
| 3 |
| A、3x-15y+4=0 |
| B、15x-3y-2=0 |
| C、15x-3y+2=0 |
| D、3x-y+1=0 |
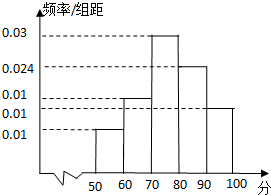 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.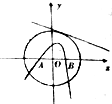 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是