题目内容
若a,b,c分别是直角三角形ABC(C为直角)内角A,B,C的对边,则直线l:ax+by+c=0被圆M:x2+y2=5所截得线段的长为 .
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:求出圆心与直线的距离,结合直角三角形的勾股定理,即可求出直线l:ax+by+c=0被圆M:x2+y2=5所截得线段的长.
解答:
解:因为Rt△ABC的两条直角边长分别为a、b,斜边长为c,
所以c2=a2+b2,
圆x2+y2=5圆心(0,0),半径为r=
,
圆心到直线ax+by+c=0的距离为:
=1,
所以直线l:ax+by+c=0被圆M:x2+y2=5所截得线段的长为2
=4.
故答案为:4.
所以c2=a2+b2,
圆x2+y2=5圆心(0,0),半径为r=
| 5 |
圆心到直线ax+by+c=0的距离为:
| |c| | ||
|
所以直线l:ax+by+c=0被圆M:x2+y2=5所截得线段的长为2
| 5-1 |
故答案为:4.
点评:本题考查直线与圆的位置关系,勾股定理的应用,考查计算能力.

练习册系列答案
相关题目
直线y=-3x+m是曲线y=x3-3x2的一条切线,则实数m的值是( )
| A、4 | B、3 | C、2 | D、1 |
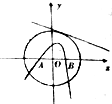 如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是
如图⊙O2:x2+y2=9,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A、B两点的抛物线以直线l为准线,则抛物线焦点的轨迹方程是