题目内容
已知函数f(x)=ex+ax(a∈R),g(x)=exlnx(e为自然对数的底数).
(Ⅰ)设曲线y=f(x)在x=1处的切线为l,点(1,0)到直线l的距离为
,求a的值;
(Ⅱ)若对于任意实数x≥0,f(x)>0恒成立,试确定实数a的取值范围;
(Ⅲ)当a=-1时,函数M(x)=g(x)-f(x)在[1,e]上是否存在极值?若存在,求出极值;若不存在,请说明理由.
(Ⅰ)设曲线y=f(x)在x=1处的切线为l,点(1,0)到直线l的距离为
| ||
| 2 |
(Ⅱ)若对于任意实数x≥0,f(x)>0恒成立,试确定实数a的取值范围;
(Ⅲ)当a=-1时,函数M(x)=g(x)-f(x)在[1,e]上是否存在极值?若存在,求出极值;若不存在,请说明理由.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)由导函数求出曲线y=f(x)在x=1处的切线l的方程,再由点(1,0)到直线l的距离为
列式求解a的值;
(Ⅱ)当x=0时,对任意实数a,f(x)=ex>0恒成立;当x>0时,由f(x)>0恒成立,分离参数a,然后
构造辅助函数Q(x)=-
,由导数求其最大值,则a的范围可求;
(Ⅲ)把f(x)和g(x)的解析式代入M(x)=g(x)-f(x),整理后求其导函数,由其导函数恒大于0得到M(x)是定义域内的增函数,从而说明函数M(x)=g(x)-f(x)在[1,e]上不存在极值.
| ||
| 2 |
(Ⅱ)当x=0时,对任意实数a,f(x)=ex>0恒成立;当x>0时,由f(x)>0恒成立,分离参数a,然后
构造辅助函数Q(x)=-
| ex |
| x |
(Ⅲ)把f(x)和g(x)的解析式代入M(x)=g(x)-f(x),整理后求其导函数,由其导函数恒大于0得到M(x)是定义域内的增函数,从而说明函数M(x)=g(x)-f(x)在[1,e]上不存在极值.
解答:
解:(Ⅰ)∵f(x)=ex+ax,
∴f′(x)=ex+a,f(1)=e+a,
y=f(x)在x=1处的切线斜率为f′(1)=e+a,
∴切线l的方程为y-(e+a)=(e+a)(x-1),即(e+a)x-y=0.
又切线l与点(1,0)距离为
,
∴
=
,
解之得,a=-e+1,或a=-e-1;
(Ⅱ)∵对于任意实数x≥0,f(x)>0恒成立,
∴若x=0,则a为任意实数时,f(x)=ex>0恒成立;
若x>0,f(x)=ex+ax>0恒成立,即a>-
在x>0上恒成立,
设Q(x)=-
,则Q′(x)=-
=
,
当x∈(0,1)时,Q′(x)>0,则Q(x)在(0,1)上单调递增.
当x∈(1,+∞)时,Q′(x)<0,则Q(x)在(1,+∞)上单调递减.
∴当x=1时,Q(x)取得最大值,Q(x)max=Q(1)=-e,
∴a的取值范围为(-e,+∞).
综上,对于任意实数x≥0,f(x)>0恒成立的实数a的取值范围为(-e,+∞);
(Ⅲ)依题意,M(x)=exlnx-ex+x,
∴M′(x)=
+exlnx-ex+1=(
+lnx-1)•ex+1,
设h(x)=
+lnx-1,则h′(x)=-
+
=
,当x∈[1,e],h′(x)≥0,
故h(x)在[1,e]上单调增函数,因此h(x)在[1,e]上的最小值为h(1)=0,
即h(x)=
+lnx-1≥h(1)=0,
又ex>0,
∴在[1,e]上,M′(x)=(
+lnx-1)•ex+1>0,
即M(x)=g(x)-f(x)在[1,e]上不存在极值.
∴f′(x)=ex+a,f(1)=e+a,
y=f(x)在x=1处的切线斜率为f′(1)=e+a,
∴切线l的方程为y-(e+a)=(e+a)(x-1),即(e+a)x-y=0.
又切线l与点(1,0)距离为
| ||
| 2 |
∴
| |(e+a)•1+(-1)•0+0| | ||
|
| ||
| 2 |
解之得,a=-e+1,或a=-e-1;
(Ⅱ)∵对于任意实数x≥0,f(x)>0恒成立,
∴若x=0,则a为任意实数时,f(x)=ex>0恒成立;
若x>0,f(x)=ex+ax>0恒成立,即a>-
| ex |
| x |
设Q(x)=-
| ex |
| x |
| xex-ex |
| x2 |
| (1-x)•ex |
| x2 |
当x∈(0,1)时,Q′(x)>0,则Q(x)在(0,1)上单调递增.
当x∈(1,+∞)时,Q′(x)<0,则Q(x)在(1,+∞)上单调递减.
∴当x=1时,Q(x)取得最大值,Q(x)max=Q(1)=-e,
∴a的取值范围为(-e,+∞).
综上,对于任意实数x≥0,f(x)>0恒成立的实数a的取值范围为(-e,+∞);
(Ⅲ)依题意,M(x)=exlnx-ex+x,
∴M′(x)=
| ex |
| x |
| 1 |
| x |
设h(x)=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| x-1 |
| x2 |
故h(x)在[1,e]上单调增函数,因此h(x)在[1,e]上的最小值为h(1)=0,
即h(x)=
| 1 |
| x |
又ex>0,
∴在[1,e]上,M′(x)=(
| 1 |
| x |
即M(x)=g(x)-f(x)在[1,e]上不存在极值.
点评:本题考查了利用导数研究曲线上某点的切线方程,考查了函数恒成立问题,训练了利用构造函数法求解字母的范围,解答的关键是熟练掌握基本初等函数的导函数,属高考试卷中的压轴题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
已知i是虚数单位,若(m+i)2=3-4i,则实数m的值为( )
| A、-2 | ||
| B、±2 | ||
C、±
| ||
| D、2 |
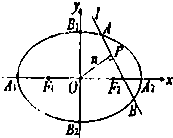 如图,椭圆C:
如图,椭圆C: