题目内容
 已知向量
已知向量| m |
| π |
| 4 |
| 3 |
| π |
| 4 |
| n |
| π |
| 4 |
| π |
| 4 |
| m |
| n |
(Ⅰ)求函数y=f(x)的图象的对称中心坐标;
(Ⅱ)将函数y=f(x)图象向下平移
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算
专题:
分析:(Ⅰ)利用平面向量的数量积的坐标运算可求得y=f(x)的解析式,利用正弦函数的性质可求得其对称中心坐标;
(Ⅱ)依题意,可求得g(x)=sin(2x+
),通过列表,描点可作出它在[-
,
]上的图象
(Ⅱ)依题意,可求得g(x)=sin(2x+
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
解答:
解:(Ⅰ)f(x)=
•
=sin2(x+
)-
cos(x+
)cos(x-
)
=
(1+sin2x)-
cos2x
=sin(2x-
)+
,…(4分)
由sin(2x-
)=0得:2x-
=kπ,k∈Z,
∴x=
kπ+
,k∈Z.
∴f(x)的图象的对称中心坐标为(
kπ+
,
),k∈Z. …(6分)
(Ⅱ)令h(x)=f(x)-
,则h(x)=sin(2x-
),
∴g(x)=h(x+
)=sin[2(x+
)-
]=sin(2x+
),
列表:
 ,
,
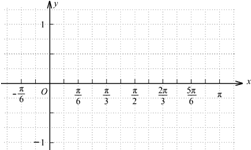
描点、连线得函数y=g(x)在[-
,
]上的图象如图所示:

…(12分)
| m |
| n |
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 3 |
| 1 |
| 2 |
由sin(2x-
| π |
| 3 |
| π |
| 3 |
∴x=
| 1 |
| 2 |
| π |
| 6 |
∴f(x)的图象的对称中心坐标为(
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(Ⅱ)令h(x)=f(x)-
| 1 |
| 2 |
| π |
| 3 |
∴g(x)=h(x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
列表:
 ,
,描点、连线得函数y=g(x)在[-
| π |
| 6 |
| 5π |
| 6 |

…(12分)
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查平面向量的数量积的坐标运算,考查列表作图能力,属于中档题.

练习册系列答案
相关题目
设全集U={x|0<x<2},集合A={x|0<x≤1},则集合∁UA=( )
| A、(0,1) |
| B、(0,1] |
| C、(1,2) |
| D、[1,2) |
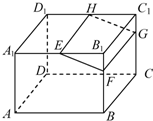 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为