题目内容
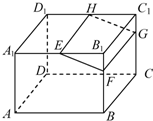 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为考点:几何概型
专题:概率与统计
分析:在长方体ABCD-A1B1C1D1中,得到几何体A1ABFE-D1DCGH和EB1F-HC1G是等高的五棱柱和三棱柱,
根据柱体的体积公式可得几何体EB1F-GC1H的体积等于长方体ABCD-A1B1C1D1体积的
,
由此利用几何概型计算公式即可算出所求的概率.
根据柱体的体积公式可得几何体EB1F-GC1H的体积等于长方体ABCD-A1B1C1D1体积的
| 1 |
| 10 |
由此利用几何概型计算公式即可算出所求的概率.
解答:
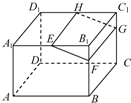 解:因为EH∥A1D1,则EH∥B1C1,所以EH∥平面B1C1CB,
解:因为EH∥A1D1,则EH∥B1C1,所以EH∥平面B1C1CB,
过EH的平面与平面B1C1CB交于FG,则EH∥FG,
所以易证明几何体A1ABFE-D1DCGH和EB1F-HC1G是等高的五棱柱和三棱柱,
由于在长方体ABCD-A1B1C1D1中,AB=2AA1=2a,EF=a,B1E=2B1F,
则B1E=
,B1F=
.
由几何概型可知,长方体内任一点取自于几何体A1ABFE-D1DCGH内的概率为:
P=1-
=1-
=1-
=
.
故答案为:
.
 解:因为EH∥A1D1,则EH∥B1C1,所以EH∥平面B1C1CB,
解:因为EH∥A1D1,则EH∥B1C1,所以EH∥平面B1C1CB,过EH的平面与平面B1C1CB交于FG,则EH∥FG,
所以易证明几何体A1ABFE-D1DCGH和EB1F-HC1G是等高的五棱柱和三棱柱,
由于在长方体ABCD-A1B1C1D1中,AB=2AA1=2a,EF=a,B1E=2B1F,
则B1E=
2
| ||
| 5 |
| ||
| 5 |
由几何概型可知,长方体内任一点取自于几何体A1ABFE-D1DCGH内的概率为:
P=1-
| V三棱柱 |
| V |
| S△EB1F |
| S矩形ABB1A1 |
| ||||||||||
| 2a2 |
| 9 |
| 10 |
故答案为:
| 9 |
| 10 |
点评:本题着重考查了正方体的性质、柱体体积公式和几何概型及其应用等知识,属于中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2013)+f(2015)的值为( )
| A、-1 | B、1 | C、0 | D、无法计算 |
 已知向量
已知向量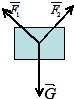 甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为