题目内容
已知f(x)满足f(x+2)•f(x)=-1,f(x)关于点(1,0)中心对称,关于直线x=a轴对称,求a的值.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:运用赋值,根据条件f(x+2)•f(x)=-1得到f(x)是最小正周期为4的函数,根据f(x)关于点(1,0)中心对称,得到f(-x)+f(2+x)=0,根据函数关于直线x=a轴对称,得到f(-x)=f(2a+x),从而得到f(2a+x)=-f(x+2),再把x换为x-2,得到f(2a-2+x)=-f(x),再把x换为x+2a-2,从而得到周期4a-4,令4a-4=4k(k是整数),求出a的值.
解答:
解:∵f(x)满足f(x+2)•f(x)=-1,
将x换为x+2得f(x+4)•f(x+2)=-1,
∴f(x+4)=f(x),
即f(x)是最小正周期为4的函数,
∵f(x)关于点(1,0)中心对称,
∴f(-x)+f(2+x)=0,
∵f(x)图象关于直线x=a对称,
∴f(-x)=f(2a+x),
∴f(2a+x)=-f(2+x),
将x换为x-2得,f(2a-2+x)=-f(x),
∴f(x+4a-4)=-f(x+2a-2)=f(x),
即函数f(x)的周期为4a-4,
∴4a-4=4k,a=1+k(k为整数).
∴a的值为1+k(k为整数).
将x换为x+2得f(x+4)•f(x+2)=-1,
∴f(x+4)=f(x),
即f(x)是最小正周期为4的函数,
∵f(x)关于点(1,0)中心对称,
∴f(-x)+f(2+x)=0,
∵f(x)图象关于直线x=a对称,
∴f(-x)=f(2a+x),
∴f(2a+x)=-f(2+x),
将x换为x-2得,f(2a-2+x)=-f(x),
∴f(x+4a-4)=-f(x+2a-2)=f(x),
即函数f(x)的周期为4a-4,
∴4a-4=4k,a=1+k(k为整数).
∴a的值为1+k(k为整数).
点评:本题主要考查函数的周期性和对称性,注意掌握解决抽象函数的常用方法:赋值法,正确赋值和赋式是解决此类问题的关键,同时牢记结论:f(x)满足f(a-x)+f(a+x)=2b,则f(x)关于点(a,b)对称;f(x)满足f(a-x)=f(a+x)=,则f(x)关于直线x=a对称.

练习册系列答案
相关题目
已知sinα+cosα=
,则sin2(
-α)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知向量
已知向量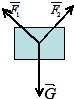 甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为