题目内容
已知定义域为R的函数f(x)=
是奇函数,并且在R上单调递减.
(1)求a,b的值;
(2)若对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.
| b-2x |
| 2x+a |
(1)求a,b的值;
(2)若对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.
考点:函数恒成立问题,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据函数性质建立条件关系即可求a,b的值;
(2)根据函数奇偶性和单调性之间的关系将不等式进行转化即可得到结论.
(2)根据函数奇偶性和单调性之间的关系将不等式进行转化即可得到结论.
解答:
解:(1)∵定义域为R的函数f(x)=
是奇函数,
∴f(0)=0,即
=0,解得b=1,
由f(-1)=-f(1)得a=1,经检验a=1,b=1符合题意. …(6分)
(2)对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,
则f(t2-2t)<-f(2t2-k),
∵f(x)为奇函数,∴-f(2t2-k)<f(k-2t2),
即不等式等价为f(t2-2t)<f(k-2t2),
∵f(x)为减函数,
∴t2-2t>k-2t2,
即k<3t2-2t恒成立,
而3t2-2t=3(t-
)2-
≥-
,
∴k<-
…(12分)
| b-2x |
| 2x+a |
∴f(0)=0,即
| b-1 |
| 1+a |
由f(-1)=-f(1)得a=1,经检验a=1,b=1符合题意. …(6分)
(2)对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,
则f(t2-2t)<-f(2t2-k),
∵f(x)为奇函数,∴-f(2t2-k)<f(k-2t2),
即不等式等价为f(t2-2t)<f(k-2t2),
∵f(x)为减函数,
∴t2-2t>k-2t2,
即k<3t2-2t恒成立,
而3t2-2t=3(t-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴k<-
| 1 |
| 3 |
点评:本题主要考查函数奇偶性和单调性的应用,以及不等式的求解,根据函数奇偶性和单调性之间的关系,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f[lg(x+1)]的定义域是(0、9],则f(x2)的定义域是( )
| A、[-1,1] |
| B、(-1,1) |
| C、[-1,0)∪(0,1] |
| D、(-1,0)∪(0,1) |
函数y=
的图象大致为( )
| cos3x |
| 3x-3-x |
A、 |
B、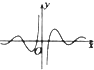 |
C、 |
D、 |
等比数列{an}的前n项和为Sn,已知a2a3=2a1,且a4与2a7的等差中项为
,则S5=( )
| 5 |
| 4 |
| A、29 | B、31 | C、33 | D、36 |