题目内容
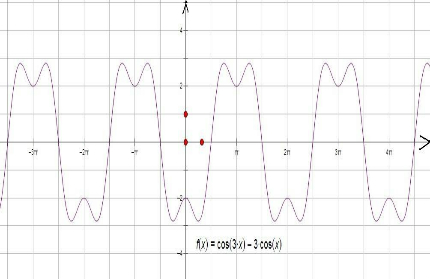
函数y=cos3x-3cosx在下列哪个区间是增函数( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(π,
|
考点:复合三角函数的单调性
专题:三角函数的图像与性质
分析:结合图象,对4个选项区间,取特殊的x1,x2值,当x1<x2时,当x1<x2时,如有y1>y2,则不是增函数,用排除法可以解决.
解答:
解:画出图象如下:
A、因为
<
,而有cos(3×
)-3cos
=-
>cos(3×
)-3cos
=-2
,故不是增函数;
B、由A知,函数在(
,
)不是增函数,(
,
)∈(
,
),故不是增函数;
D、因为π<
<
,而有cos(
×3)-3cos
=2
>cos(
×3)-3cos
=
,故不是增函数;
故选:C.
A、因为
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 2 |
B、由A知,函数在(
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| 3π |
| 4 |
D、因为π<
| 5π |
| 4 |
| 4π |
| 3 |
| 5π |
| 4 |
| 5π |
| 4 |
| 2 |
| 4π |
| 3 |
| 4π |
| 3 |
| 5 |
| 2 |
故选:C.

点评:本题主要考察了复合三角函数的单调性,是选择题可以用排除法解决,属于中档题.

练习册系列答案
相关题目
把89转化为五进制数是( )
| A、324(5) |
| B、253(5) |
| C、342(5) |
| D、423(5) |
已知函数y=f(x)在区间[-5,5]上是增函数,那么下列不等式中成立的是( )
| A、f(4)>f(-π)>f(3) |
| B、f(π)>f(4)>f(3) |
| C、f(4)>f(3)>f(π) |
| D、f(-3)>f(-π)>f(-4) |