题目内容
下列函数中,是奇函数的是( )
| A、y=2x |
| B、y=-3x2+1 |
| C、y=x3-x |
| D、y=3x2+1 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:函数奇偶性的判定必须首先要求定义域,如果关于原点对称,再利用等于判定.
解答:
解:观察四个选项,函数的定义域都是R,
其中对于A,是非奇非偶的函数,对于B,D都满足f(-x)=f(x),是偶函数,对于C,f(-x)=-f(x),是奇函数;
故选C.
其中对于A,是非奇非偶的函数,对于B,D都满足f(-x)=f(x),是偶函数,对于C,f(-x)=-f(x),是奇函数;
故选C.
点评:本题考查了函数奇偶性的判定,在定义域关于原点对称的情况下,利用f(-x)与f(x)的关系判断奇偶性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果不等式|x-a|<1成立的充分不必要条件是1<x<2,则实数a的取值范围是( )
| A、1<a<2 |
| B、1≤a≤2 |
| C、a>2或a<1 |
| D、a≥2或a≤1 |
从2010名学生中选50人组成参观团,先用简单随机抽样方法剔除10人,再将其余2000人按系统抽样方法选取,则每人入选的概率( )
| A、不全相等 | ||
| B、B均不相等 | ||
C、都是
| ||
D、都是
|
复数z=i2(1-i)(其中i为虚数单位)的值是( )
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
已知函数f(x)=2x-
,则在下列区间中,使f(x)有零点的区间是( )
| 1 |
| x |
| A、(1,+∞) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
不等式
>1的解集为( )
| 2 |
| x-1 |
| A、{x|x>3} |
| B、{x|1<x<3} |
| C、{x|x<3} |
| D、{x|x<3或x>1} |
已知复数z=a2-1+(a+1)i(a∈R)为纯虚数,则
为( )
. |
| z |
| A、0 | B、2i |
| C、-2i | D、-1-2i |
设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)<0},则图中阴影部分表示的集合为( )
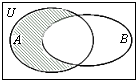

| A、{x|0<x≤1} |
| B、{x|1≤x<2} |
| C、{x|x≥1} |
| D、{x|x≤1} |