题目内容
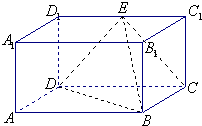 长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.
长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.1)求证:平面BCE⊥平面BDE;
2)求点C到平面BDE的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明平面BCE⊥平面BDE,只要证明DE⊥平面EBC,只要证明由EC⊥ED,BC⊥DE,即可证明.
(2)由VC-EBD=VE-BCD可求C到平面BDE的距离.
(2)由VC-EBD=VE-BCD可求C到平面BDE的距离.
解答:
(1)证明:由题意可得,EC=ED=
a
∵CD=2a
∴EC⊥ED,
∵BC⊥平面CC1D1D
∴BC⊥DE,
即DE垂直于平面EBC中两条相交直线,
因此DE⊥平面EBC,
∵DE?平面BDE,
∴平面BCE⊥平面BDE;
(2)解:结合第(1)问得DB=
a,DE=
a,BE=
a,DE⊥BE,
所以,S△EBD=
×
a×
a=
a2
又由VC-EBD=VE-BCD得
h×
a2=
a3
故C到平面BDE的距离为h=
a.
| 2 |
∵CD=2a
∴EC⊥ED,
∵BC⊥平面CC1D1D
∴BC⊥DE,
即DE垂直于平面EBC中两条相交直线,
因此DE⊥平面EBC,
∵DE?平面BDE,
∴平面BCE⊥平面BDE;
(2)解:结合第(1)问得DB=
| 5 |
| 2 |
| 3 |
所以,S△EBD=
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
又由VC-EBD=VE-BCD得
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
故C到平面BDE的距离为h=
| ||
| 3 |
点评:本题主要考查了线面垂直的判定定理的应用,等体积求解点到面的距离的应用.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
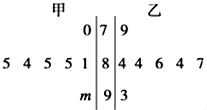 如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )
如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )| A、a1>a2 |
| B、a1<a2 |
| C、a1=a2 |
| D、a1,a2的大小与m的值有关 |
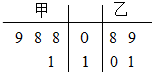 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.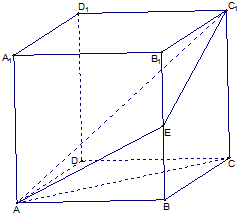 正方体AC1中AB=2,E为BB1的中点.
正方体AC1中AB=2,E为BB1的中点.