题目内容
已知函数f(x)=
.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)证明:曲线f(x)与g(x)=
-
没有公共点;
(Ⅲ)设A(x1,f(x1)),B(x2,f(x2))为曲线f(x)上的两点,且x1<x2,若曲线f(x)在点A、B处的切线重合,求实数a的取值范围.
|
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)证明:曲线f(x)与g(x)=
| 2x-1 |
| 1 |
| 2 |
(Ⅲ)设A(x1,f(x1)),B(x2,f(x2))为曲线f(x)上的两点,且x1<x2,若曲线f(x)在点A、B处的切线重合,求实数a的取值范围.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:(Ⅰ) 由二次函数和对数函数的单调性可得;(Ⅱ) 由定义域可得f(x)=lnx,令h(x)=g(x)-f(x),求导函数可判h(x)=g(x)-f(x)在[
,+∞)上是增函数,可得g(x)>f(x),即可得结论;(Ⅲ)可得x1<0<x2,写出切线,可得a=
+ln
-1=
-ln(2x1+2)-1,设h(x1)=
-ln(2x1+2)-1(-1<x1<0),导数法可得范围.
| 1 |
| 2 |
| x | 2 1 |
| 1 |
| 2x1+2 |
| x | 2 1 |
| x | 2 1 |
解答:
解:(Ⅰ)∵二次函数y=x2+2x+a对称轴为x=-1,图象开口向上,
∴二次函数y=x2+2x+a在(-∞,-1)上单调递减,在[-1,0)上单调递增,
由对数函数的性质可知y=lnx在(0,+∞)上单调递增,
∴函数f(x)的单调递减区间为(-∞,-1),单调递增区间为[-1,0)和(0,+∞);
(Ⅱ) 由g(x)有意义知x≥
,∴f(x)=lnx,
令h(x)=g(x)-f(x),求导函数可得h′(x)=
-
,
∵
≥
?x≥
?x2≥2x-1?(x-1)2≥0成立,
∴
≥
成立,∴h′(x)≥0,即h(x)=g(x)-f(x)在[
,+∞)上是增函数,
∴h(x)min=h(
)=-
-ln
=ln2-
>ln
-
=0,
∴g(x)>f(x),即函数f(x)与g(x)=
-
没有公共点;
(Ⅲ)当x1<x2<0或x2>x1>0时,f′(x1)≠f′(x2),故x1<0<x2.
当x1<0时,函数f(x)的图象在点(x1,f(x1))处的切线方程为y-(
+2x1+a)=(2x1+2)(x-x1),即y=(2x1+2)x-
+a.
当x2>0时,函数f(x)的图象在点(x2,f(x2))处的切线方程为y-lnx2=
(x-x2),即y=
•x+lnx2-1,
两切线重合的充要条件是
,由(1)及x1<0<x2,知-1<x1<0.
由(1)(2)得a=
+ln
-1=
-ln(2x1+2)-1.
设h(x1)=
-ln(2x1+2)-1(-1<x1<0),则h′(x1)=2x1-
<0.
∴h(x1)(-1<x1<0)是减函数,∴h(x1)>h(0)=-ln2-1,∴a>-ln2-1.
又当x1∈(-1,0)且趋近于-1时,h(x1)无限增大,∴a的取值范围是(-ln2-1,+∞).
故当函数f(x)的图象在点A、B处的切线重合时,a的取值范围是(-ln2-1,+∞).
∴二次函数y=x2+2x+a在(-∞,-1)上单调递减,在[-1,0)上单调递增,
由对数函数的性质可知y=lnx在(0,+∞)上单调递增,
∴函数f(x)的单调递减区间为(-∞,-1),单调递增区间为[-1,0)和(0,+∞);
(Ⅱ) 由g(x)有意义知x≥
| 1 |
| 2 |
令h(x)=g(x)-f(x),求导函数可得h′(x)=
| 1 | ||
|
| 1 |
| x |
∵
| 1 | ||
|
| 1 |
| x |
| 2x-1 |
∴
| 1 | ||
|
| 1 |
| x |
| 1 |
| 2 |
∴h(x)min=h(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| e |
| 1 |
| 2 |
∴g(x)>f(x),即函数f(x)与g(x)=
| 2x-1 |
| 1 |
| 2 |
(Ⅲ)当x1<x2<0或x2>x1>0时,f′(x1)≠f′(x2),故x1<0<x2.
当x1<0时,函数f(x)的图象在点(x1,f(x1))处的切线方程为y-(
| x | 2 1 |
| x | 2 1 |
当x2>0时,函数f(x)的图象在点(x2,f(x2))处的切线方程为y-lnx2=
| 1 |
| x2 |
| 1 |
| x2 |
两切线重合的充要条件是
|
由(1)(2)得a=
| x | 2 1 |
| 1 |
| 2x1+2 |
| x | 2 1 |
设h(x1)=
| x | 2 1 |
| 1 |
| x1+1 |
∴h(x1)(-1<x1<0)是减函数,∴h(x1)>h(0)=-ln2-1,∴a>-ln2-1.
又当x1∈(-1,0)且趋近于-1时,h(x1)无限增大,∴a的取值范围是(-ln2-1,+∞).
故当函数f(x)的图象在点A、B处的切线重合时,a的取值范围是(-ln2-1,+∞).
点评:本题考查函数的单调性,以及导数的应用和切线问题,涉及分类讨论的思想,属难题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
执行如图所示的程序框图,若输出的结果为35,则判断框中应填( )


| A、n≤5? | B、n>5? |
| C、n≤4? | D、n>4? |
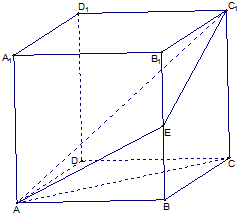 正方体AC1中AB=2,E为BB1的中点.
正方体AC1中AB=2,E为BB1的中点.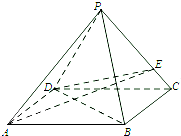 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2