题目内容
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.(1)求证:EF∥平面ABCD;
(2)求EF与平面BB1C1C所成的角.
考点:直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)线面平行判定定理即可证明;(2)EF∥AC,EF与平面BB1C1C所成的角与AC与平面BB1C1C相等,∠ACB即是.
解答:
(1)证明:连接AC,在△D1AC中,E、F分别为AD1,CD1中点,∴EF∥AC,AC?平面ABCD,EF?平面ABCD,∴EF∥平面ABCD;
(2)解:由(1)知,EF∥AC,EF与平面BB1C1C所成的角与AC与平面BB1C1C相等.∵正方体ABCD-A1B1C1D1,∴AB⊥平面BB1C1C,∠ACB即是AC与平面BB1C1C所成的角,∴∠ACB=45°
(2)解:由(1)知,EF∥AC,EF与平面BB1C1C所成的角与AC与平面BB1C1C相等.∵正方体ABCD-A1B1C1D1,∴AB⊥平面BB1C1C,∠ACB即是AC与平面BB1C1C所成的角,∴∠ACB=45°
点评:本题考查线面平行的判定及直线与平面所成的角.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
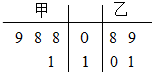 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示. 已知变量x,y满足
已知变量x,y满足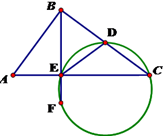 如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为
如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为