题目内容
在同一坐标系中画出函数y=ax,y=x+a的图象,可能正确的是( )
A、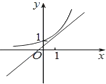 |
B、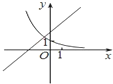 |
C、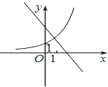 |
D、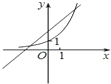 |
考点:函数的图象
专题:函数的性质及应用
分析:把a看做直线y=x+a在y轴上的截距,对应函数y=x+a单调递增,而函数y=ax当a>1时单调递增,当0<a<1时,函数y=ax单调递减,
用以上两条选出答案.
用以上两条选出答案.
解答:
解:∵a为直线y=x+a在y轴上的截距,对应函数y=x+a单调递增,
又∵当a>1时,函数y=ax单调递增,当0<a<1时,函数y=ax单调递减,
A中,从图象上看,y=ax的a满足a>1,而直线y=x+a的截距a<1,不符合以上两条,
B中,从图象上看,y=ax的a满足0<a<1,而直线y=x+a的截距a>1,不符合以上两条,
C中,从图象上看,y=ax的a满足a>1,而函数y=x+a单调递减,不符合以上两条,
∴只有选项D的图象符合以上两条,
故选:D
又∵当a>1时,函数y=ax单调递增,当0<a<1时,函数y=ax单调递减,
A中,从图象上看,y=ax的a满足a>1,而直线y=x+a的截距a<1,不符合以上两条,
B中,从图象上看,y=ax的a满足0<a<1,而直线y=x+a的截距a>1,不符合以上两条,
C中,从图象上看,y=ax的a满足a>1,而函数y=x+a单调递减,不符合以上两条,
∴只有选项D的图象符合以上两条,
故选:D
点评:本题主要考查函数的单调性及函数的图象,特别是我们常见函数的性质与图象要熟记,是基础题.

练习册系列答案
相关题目
在直角边长为1,的等腰直角三角形ABC中,D为斜边AB的中点,则
•
等于( )
| CD |
| CA |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
若x>0,y>0,且lgx+lgy=1,则
+
的最小值为( )
| 2 |
| x |
| 5 |
| y |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
对于正整数a,若存在正整数b,使得a=bn(n∈N+)则a是n次方数,其中2次方数也叫平方数,则“正整数a是平方数”是“正整数a是4次方数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在{an}为等比数列中,an>0,a2a4+2a3a5+a52=16,那么a3+a5=( )
| A、±4 | B、4 | C、2 | D、8 |
已知集合A={1,2,3,4},B={3,4,5,6},若A∩B={a,b},则a+b=( )
| A、6 | B、7 | C、8 | D、9 |