题目内容

在直角边长为1，的等腰直角三角形ABC中，D为斜边AB的中点，则
CD
•
CA
等于（　　）
A、
1
4
B、
2
2
C、
1
2
D、1
考点：平面向量数量积的运算
专题：平面向量及应用
分析：
CD
•
CA
=|
CD
|•|
CA
|cos∠DCA，运用几何图形求解线段长度，代入求解答案．
解答： 解：∵在直角边长为1，的等腰直角三角形ABC中，D为斜边AB的中点
∴|
CD
|=
2
2
，∠DCA=45°．
所以
CD
•
CA
=|
CD
|•|
CA
|cos∠DCA=
2
2
×1×
2
2
=
1
2



故选：C
点评：本题考查了向量的数量积的运算，借助几何图形求解．
练习册系列答案
相关题目
设x，y，z为空间不同的直线或不同的平面，且直线不在平面内，下列说法中能保证“若x⊥z，y⊥z，则x∥y”为真命题的序号有
 
．（把所有的真命题全填上）
①x为直线，y，z为平面；
②x，y，z都为平面；
③x，y为直线，z为平面；
④x，y，z都为直线；
⑤x，y为平面，z为直线．
已知等差数列{an}的前n项和为Sn（n∈N+），且an=2n+λ，若数列{Sn}在n≥7时为递增数列，则实数λ的取值范围为（　　）
A、（-15，+∞）
B、[-15，+∞）
C、[-16，+∞）
D、（-16，+∞）
已知A（-1，0），B（1，0），动点P（x，y）满足：|PA|+|PB|=4，则点P的轨迹的方程是
 
．
已知函数f（x）=tan（2x+
π
4
）．
（1）求f（x）的定义域与最小正周期；
（2）设α∈（0，
π
4
），若f（
α
2
）=2cos 2α，求α的大小．
已知公差不为0的等差数列{an}的前n项和为Sn，S4=16 a22=a1a5 
（1）求若数列{an}通项公式；
（2）若数列满足bn=an+2n，求数列{bn}的前n项和Tn．
已知f（x）=
(a-3)x+5，x≤1
2a
x
，
  x＞1
对任意x1，x2∈R，（x1-x2）（f（x1）-f（x2））＜0，则a的取值范围是（　　）
A、（0，3）
B、（0，3]
C、（0，2）
D、（0，2]
在数列{an}中，a1=3，2an+1=an+1，则a2=
 
．
在同一坐标系中画出函数y=ax，y=x+a的图象，可能正确的是（　　）
A、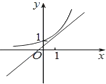
B、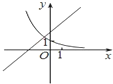
C、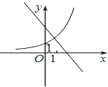
D、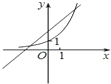

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网