题目内容

已知D是△OAB的边OA的中点，E是边AB的一个三等分点，且
AE
EB
=2，若向量
OA
=
a
，
DE
=
b
，试用
a
，
b
表示向量
OB
=
 
．
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：根据题意，画出图形，结合图形，得出AE与AB的关系；求出向量
AE
，从而得出
OB
．
解答： 解：如图所示，
∵AD=DB，
AE
EB
=2，
∴AE=
2
3
AB；
又∵
OA
=
a
，
DE
=
b
，
∴
AE
=
DE
-
DA
=
b
-
1
2
a
，
OB
=
OA
+
AB
=
a
+
3
2
（
b
-
1
2
a
）=
1
4
a
+
3
2
b
．
故答案为：
1
4
a
+
3
2
b
．
点评：本题考查了平面向量的应用问题，解题时应根据题意，画出图形，结合图形解答问题，是基础题．
练习册系列答案
相关题目
已知f（x）=
(a-3)x+5，x≤1
2a
x
，
  x＞1
对任意x1，x2∈R，（x1-x2）（f（x1）-f（x2））＜0，则a的取值范围是（　　）
A、（0，3）
B、（0，3]
C、（0，2）
D、（0，2]
偶函数f（x）的定义域为R，若f（-x+1）=f（x+1），且f（1）=1，f（0）=0则f（4）+f（5）=（　　）
A、2B、-1C、0D、1
在同一坐标系中画出函数y=ax，y=x+a的图象，可能正确的是（　　）
A、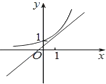
B、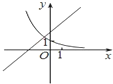
C、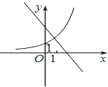
D、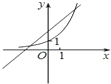
如果执行如图程序框图（判断条件k≤20？），那么输出的S=
 
．
给出四个函数；（1）y=x3+x（2）y=
1
x
（x＞0）（3）y=
x2+2
x
（4）y=x2+1，其中奇函数的个数是（　　）
A、1B、2C、3D、4
设集合A={x|-1≤x≤2}，B={x|x2-（2m+1）x+2m＜0}．
（1）当m＜
1
2
时，求集合B；
（2）若A∪B=A，求实数m的取值范围．
在△ABC中，A，B，C为内角，且sinAcosA=sinBcosB，则△ABC是（　　）三角形．
A、等腰B、直角
C、等腰且直角D、等腰或直角
复数1-2i的虚部是（　　）
A、-2iB、2iC、-2D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网