题目内容
在△ABC中,三个内角A、B、C对应的边分别为a、b、c,
(Ⅰ)若A、B、C成等差数列,且a、b、c成等比数列,求证:△ABC为等边三角形;
(Ⅱ)若cosA、cosB、cosC成等比数列,a、b、c成等比数列,求证:△ABC为等边三角形.
(Ⅰ)若A、B、C成等差数列,且a、b、c成等比数列,求证:△ABC为等边三角形;
(Ⅱ)若cosA、cosB、cosC成等比数列,a、b、c成等比数列,求证:△ABC为等边三角形.
考点:余弦定理的应用,三角形的形状判断
专题:解三角形
分析:(Ⅰ)通过A、B、C成等差数列,且a、b、c成等比数列,结合正弦定理以及余弦定理即可证明△ABC为等边三角形;
(Ⅱ)利用cosA、cosB、cosC成等比数列,a、b、c成等比数列,通过正弦定理以及余弦定理即可证明△ABC为等边三角形.
(Ⅱ)利用cosA、cosB、cosC成等比数列,a、b、c成等比数列,通过正弦定理以及余弦定理即可证明△ABC为等边三角形.
解答:
解:(Ⅰ)在△ABC中,若A、B、C成等差数列,则2B=A+C,又A+B+C=π
所以B=
…(2分)
因为a、b、c成等比数列,所以b2=ac…(4分)
故由a2+c2-2accosB=b2有a2+c2-2ac=0,所以a=c…(6分)
所以△ABC为等边三角形…(7分)
(Ⅱ)在△ABC中,因为cosA、cosB、cosC成等比数列
所以cos2B=cosA•cosC…(8分)
因为a、b、c成等比数列,所以b2=ac
由正弦定理有sin2B=sinA•sinC…(10分)
所以cosA•cosC+sinA•sinC=1即cos(A-C)=1…(11分)
所以A=C…(12分)
所以a=c,且b2=ac,所以a=c=b…(13分)
故△ABC为等边三角形…(14分)
所以B=
| π |
| 3 |
因为a、b、c成等比数列,所以b2=ac…(4分)
故由a2+c2-2accosB=b2有a2+c2-2ac=0,所以a=c…(6分)
所以△ABC为等边三角形…(7分)
(Ⅱ)在△ABC中,因为cosA、cosB、cosC成等比数列
所以cos2B=cosA•cosC…(8分)
因为a、b、c成等比数列,所以b2=ac
由正弦定理有sin2B=sinA•sinC…(10分)
所以cosA•cosC+sinA•sinC=1即cos(A-C)=1…(11分)
所以A=C…(12分)
所以a=c,且b2=ac,所以a=c=b…(13分)
故△ABC为等边三角形…(14分)
点评:本题考查三角形的形状的判断与证明,正弦定理以及余弦定理,数列的基本知识的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N+),且an=2n+λ,若数列{Sn}在n≥7时为递增数列,则实数λ的取值范围为( )
| A、(-15,+∞) |
| B、[-15,+∞) |
| C、[-16,+∞) |
| D、(-16,+∞) |
已知f(x)=
对任意x1,x2∈R,(x1-x2)(f(x1)-f(x2))<0,则a的取值范围是( )
|
| A、(0,3) |
| B、(0,3] |
| C、(0,2) |
| D、(0,2] |
在同一坐标系中画出函数y=ax,y=x+a的图象,可能正确的是( )
A、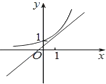 |
B、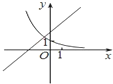 |
C、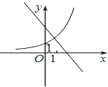 |
D、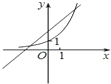 |
在△ABC中,A,B,C为内角,且sinAcosA=sinBcosB,则△ABC是( )三角形.
| A、等腰 | B、直角 |
| C、等腰且直角 | D、等腰或直角 |

