题目内容
在{an}为等比数列中，an＞0，a2a4+2a3a5+a52=16，那么a3+a5=（ ）
| A、±4 | B、4 | C、2 | D、8 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：利用等比数列的性质结合已知得到(a3+a5)2=16，再由an＞0求得a3+a5．
解答：
解：∵数列{an}为等比数列中，由a2a4+2a3a5+a52=16，得
a32+2a3a5+a52=16，
即(a3+a5)2=16．
∵an＞0，
∴a3+a5=4．
故选：B．
a32+2a3a5+a52=16，
即(a3+a5)2=16．
∵an＞0，
∴a3+a5=4．
故选：B．
点评：本题考查了等比数列的通项公式，考查了等比数列的性质，是基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
在同一坐标系中画出函数y=ax，y=x+a的图象，可能正确的是（ ）
A、 |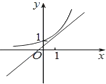
B、 |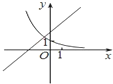
C、 |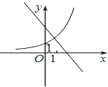
D、 |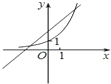
设Tn是等比数列{an}的前n项之积，若T5=
，且a2=
，则等比数列{an}的公比q为（ ）
| 1 |
| 32 |
| 1 |
| 4 |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
在△ABC中，A，B，C为内角，且sinAcosA=sinBcosB，则△ABC是（ ）三角形．
| A、等腰 | B、直角 |
| C、等腰且直角 | D、等腰或直角 |
执行如图所示的程序框图，若输入x的值是36，输出y的值是9，则①处的式子可以是（ ）
A、y=（
| |||
| B、y=3x | |||
| C、y=x | |||
D、y=-
|
函数y=4-x-
（x＞0）的最大值是（ ）
| 1 |
| x |
| A、5 | ||
| B、4 | ||
C、
| ||
| D、2 |