题目内容
若x>0,y>0,且lgx+lgy=1,则
+
的最小值为( )
| 2 |
| x |
| 5 |
| y |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:根据对数的基本运算,结合基本不等式即可得到结论.
解答:
解:∵lgx+lgy=1,
∴lgxy=1,且x>0,y>0,
即xy=10,
∴
+
≥2
=2,
当且仅当
=
,即x=2,y=5时取等号,
故选:C.
∴lgxy=1,且x>0,y>0,
即xy=10,
∴
| 2 |
| x |
| 5 |
| y |
|
当且仅当
| 2 |
| x |
| 5 |
| y |
故选:C.
点评:本题主要考查不等式的应用,利用对数的基本运算求出xy=10是解决本题的关键,比较基础.

练习册系列答案
相关题目
在同一坐标系中画出函数y=ax,y=x+a的图象,可能正确的是( )
A、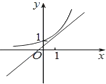 |
B、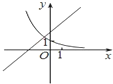 |
C、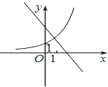 |
D、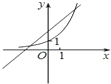 |
