Question

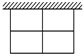如图所示：用篱笆围成一个一边靠墙的矩形菜园，假设墙有足够长．
（Ⅰ） 若篱笆的总长为30m，则这个矩形的长，宽各为多少时，菜园的面积最大？
（Ⅱ） 若菜园的面积为32m²，则这个矩形的长，宽各为多少时，篱笆的总长最短？

Answer 1

考点：基本不等式在最值问题中的应用

专题：应用题,不等式的解法及应用

分析：（Ⅰ）根据篱笆的总长为30米，可得x+2y=30，利用基本不等式，即可求面积的最值；
（Ⅱ）由条件知S=xy=32，l=x+2y，利用基本不等式，即可得出结论．

解答： 解：设这个矩形的长为xm，宽为ym，篱笆的长为lm，面积为Sm²．
（Ⅰ） 由题知x+2y=30，由于x+2y≥2

x•2y

=2

2xy

，
∴，⇒xy≤

225

2

，即S≤

225

2

，当且仅当x=2y时等号成立．
由

x+2y=30 x=2y

⇒

x=15 y=7.5

故这个矩形的长为15m，宽为7.5m时，菜园的面积最大．
（Ⅱ） 条件知S=xy=32，l=x+2y．∵x+2y≥2

2xy

=16，当且仅当x=2y时等号成立．
由

x=2y xy=32

⇒

x=8 y=4

故这个矩形的长为8m、宽为4m时，可使篱笆的总长最短．

点评：本题考查基本不等式在最值问题中的应用，考查利用数学知识解决实际问题，考查学生分析解决问题的能力．