题目内容
关于z的方程|z+2i|=|z-2i|+4在复平面上是什么图形（ ）
| A、椭圆 | B、双曲线 | C、直线 | D、射线 |
考点：复数求模
专题：数系的扩充和复数
分析：设复平面上A（0，-2），B（0，2），点P（a，b）对应的复数z=a+bi（a，b∈R），依题意，可知|PA|-|PB|=|AB|=4，从而可得答案．
解答：
解：设复平面上A（0，-2），B（0，2），点P（a，b）对应的复数z=a+bi（a，b∈R），
∵|z+2i|=|z-2i|+4，
∴|z+2i|-|z-2i|=4，
∴|PA|-|PB|=|AB|=4，
∴动点P的轨迹是从B点出发的射线（方向为
），
故选：D．
∵|z+2i|=|z-2i|+4，
∴|z+2i|-|z-2i|=4，
∴|PA|-|PB|=|AB|=4，
∴动点P的轨迹是从B点出发的射线（方向为
| AB |
故选：D．
点评：本题考查复数的模的几何意义，考查等价转化思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
曲线y=x3+x-2在P点处的切线平行于直线y=4x-1，则此切线方程是（ ）
| A、y=4x |
| B、y=4x-4 |
| C、y=4x+8 |
| D、y=4x或y=4x-4 |
设
、
、
是非零向量，则下列结论正确是（ ）
| a |
| b |
| c |
A、（
| ||||||||||||
B、若
| ||||||||||||
C、若
| ||||||||||||
D、|
|
已知函数f（x）=x3-ax2-1在x=2处取得极值，则实数a等于（ ）
| A、1 | B、2 | C、3 | D、4 |
已知集合M满足{1，2}⊆M⊆{1，2，3，4，5}，这样的集合M有（ ）个．
| A、7 | B、8 | C、9 | D、10 |
函数f（x）=x2-2lnx的递减区间是（ ）
| A、（-1，1） |
| B、（0，1） |
| C、（-∞，-1），（0，1） |
| D、（-1，0），（0，1） |
已知线段AB的长为4，以AB为直径的圆有一内接梯形ABCD，且AB∥CD，若椭圆以A、B为焦点，且经过点C、D，则该椭圆的离心率的范围是（ ）A、（0，
| ||||||
B、（0，
| ||||||
C、（
| ||||||
D、（
|
已知命题“若p则￢q”是真命题，则下列命题中一定是真命题的为（ ）
| A、若￢p则q |
| B、若￢q则p |
| C、若q则￢p |
| D、若￢p则￢q |
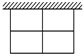如图所示：用篱笆围成一个一边靠墙的矩形菜园，假设墙有足够长．