题目内容
7.已知定义在R上的奇函数f(x)满足f(x+3)=f(x),且当x∈[0,$\frac{3}{2}$)时,f(x)=一x3.则f($\frac{11}{2}$)=( )| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{125}{8}$ | D. | $\frac{125}{8}$ |
分析 根据函数奇偶性和条件求出函数是周期为3的周期函数,利用函数周期性和奇偶性的关系进行转化即可得到结论.
解答 解:∵奇函数f(x)满足f(x+3)=f(x),
∴函数f(x)是周期为3的函数,
∵当x∈[0,$\frac{3}{2}$)时,f(x)=-x3,
∴f($\frac{11}{2}$)=f($\frac{11}{2}$-6)=f(-$\frac{1}{2}$)=-f($\frac{1}{2}$)=$\frac{1}{8}$,
故选:B.
点评 本题主要考查函数值的计算,根据条件求出函数的周期性,利用函数的奇偶性和周期性进行转化是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
18.已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$,N={x|-1<x<1},则( )
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
2.命题“若a>b,则a+c>b+c”的逆命题是( )
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
19.设集合$A=[(x,y)|\frac{x^2}{25}+\frac{y^2}{16}≤1],B=[(x,y)|\left\{\begin{array}{l}|x|≤m\\|y|≤n\end{array}\right.,0<m<5,0<n<4且(m,n)∈A]$,则集合∁AB对应图形面积取得最小值时,m+n的值为( )
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
9.已知直角△ABC中,AB=3,AC=4,BC=5,I是△ABC的内心,P是△IBC内部(不含边界)的动点,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的取值范围是( )
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
10.执行如图所示的程序框图,若输入x=20,则输出的y的值为( )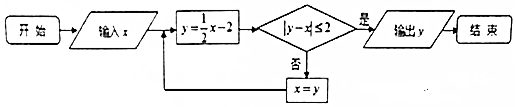

| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |
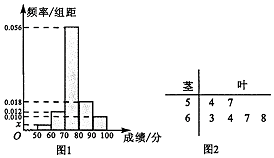 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.