题目内容
13.已知P是△ABC所在平面内一点,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 根据P是△ABC所在平面内一点,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,得点P是△ABC的重心.再根据几何概型公式,将△PBC的面积与△ABC的面积相除可得本题的答案.
解答 解:∵P是△ABC所在平面内一点,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,
∴P是△ABC的重心,
∴点P到BC的距离等于A到BC的距离的$\frac{1}{3}$.
∴S△PBC=$\frac{1}{3}$S△ABC,
将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为P=$\frac{1}{3}$.
故选B.
点评 本题考查的知识点是几何概型概率计算公式,计算出满足条件和所有基本事件对应的几何量,是解答的关键,难度中档.

练习册系列答案
相关题目
8.直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为$2\sqrt{3}$,则直线的斜率为( )
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
5.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x<2}\\{\frac{1}{3}{x}^{2}-\frac{8}{3}x+5,x≥2}\end{array}\right.$,若函数y=f(x)-m(m∈R)有四个零点x1,x2,x3,x4,则x1x2x3x4的取值范围是( )
| A. | (7,12) | B. | (12,15) | C. | (12,16) | D. | (15,16) |
2.下列函数在(0,+∞)上是增函数的是( )?
| A. | y=ln(x-2) | B. | y=-$\sqrt{x}$ | C. | y=x2 | D. | y=$\frac{1}{x}$ |
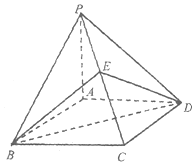 如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点. 已知抛物线x2=4y,圆C:x2+(y-2)2=4,点M(x0,y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1,k2
已知抛物线x2=4y,圆C:x2+(y-2)2=4,点M(x0,y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1,k2