题目内容
3.已知函数f(x)=x2+2x-3,g(x)=$\frac{klnx}{x}$,且函数f(x)与g(x)的图象在x=1处的切线相同.(1)求k的值;
(2)令F(x)=$\left\{\begin{array}{l}{|f(x)|(x≤1)}\\{g(x)(x>1)}\end{array}\right.$,若函数y=F(x)-m存在3个零点,求实数m的取值范围.
分析 (1)求出函数f(x)的导数f′(x)=2x+2,求出切线方程,利用函数f(x)与g(x)的图象在x=1处的切线相同,列出关系式求解即可.
(2)化简F(x)=$\left\{\begin{array}{l}{|f(x)|(x≤1)}\\{g(x)(x>1)}\end{array}\right.$=$\left\{\begin{array}{l}{|{x}^{2}+2x-3|,x≤1}\\{\frac{4lnx}{x},x>1}\end{array}\right.$,通过当x>1时,函数的图形的变化情况,求出函数的极值,画出函数的图象,然后求解m的取值范围.
解答 (本小题满分12分)
解:(1)已知函数f(x)=x2+2x-3,
函数f′(x)=2x+2,则f′(1)=4,又f(1)=0,所以f(x)在x=1处的切线方程为y=4x-4,
又因为函数f(x)与g(x)的图象在x=1处的切线相同,g′(x)=$\frac{k(1-lnx)}{{x}^{2}}$,
所以g′(1)=k=4.(4分)
(2)令F(x)=$\left\{\begin{array}{l}{|f(x)|(x≤1)}\\{g(x)(x>1)}\end{array}\right.$=$\left\{\begin{array}{l}{|{x}^{2}+2x-3|,x≤1}\\{\frac{4lnx}{x},x>1}\end{array}\right.$,
当x>1时,F(x)=$\frac{4lnx}{x}$,F′(x)=$\frac{4-4lnx}{{x}^{2}}$,可得函数F(x)在x=e处的极大值为:$\frac{4}{e}$,
当x→+∞时,图象趋近于x轴.
函数F(x)的大致图象如图所示,
可知函数y=F(x)-m存在3个零点时,
m的取值范围是($\frac{4}{e}$,4).(12分)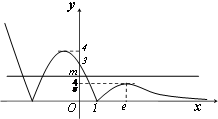
点评 本小题主要考查函数与导数的知识,具体涉及到导数的运算,用导数来研究函数的单调性等,以及函数图象的判定,考查学生解决问题的综合能力.

 阅读快车系列答案
阅读快车系列答案| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(2)从第(1)问抽取的4位居民中随机抽取2位,恰有1男1女的概率是多少;
(3)由以上数据,能否有99%的把握认为在20:00-22:00时间段的休闲方式与性别有关系.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | (-2,1) | B. | (-∞,-2)U(2,+∞) | C. | (-2,2) | D. | (-∞,-2)U(-1,1)U(2,+∞) |
| A. | a1,a2,a3成等比数列 | B. | a2,a3,a6成等比数列 | ||
| C. | a3,a4,a8成等比数列 | D. | a4,a6,a9成等比数列 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |