题目内容
18.已知函数f(x)=|x|,则下列与函数y=f(x)相等的函数是(2)(4);(1)g(x)=($\sqrt{x}$)2;(2)h(x)=$\sqrt{{x}^{2}}$;(3)s(x)=x;(4)y=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$.
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是相等函数.
解答 解:对于(1),函数g(x)=($\sqrt{x}$)2=x(x≥0),与函数f(x)=|x|(x∈R)的定义域不同,不是相等函数;
对于(2),函数g(x)=$\sqrt{{x}^{2}}$=|x|(x∈R),与函数f(x)=|x|(x∈R)的定义域相同,对应关系也相同,是相等函数;
对于(3),函数s(x)=x(x∈R),与函数f(x)=|x|(x∈R)的对应关系不相同,不是相等函数;
对于(4),函数y=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$=|x|(x∈R),与函数f(x)=|x|(x∈R)的定义域相同,对应关系也相同,是相等函数;
综上,相等的函数是(2)(4).
故答案为:(2)(4).
点评 本题考查了判断两个函数是相等函数的应用问题,是基础题目.

练习册系列答案
相关题目
13.已知P是△ABC所在平面内一点,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
19.已知f(x)=asin2x-$\frac{1}{3}$sin3x(a为常数),在x=$\frac{π}{3}$处取得极值,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $-\frac{1}{2}$ |
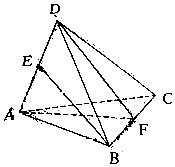 如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.