题目内容
4.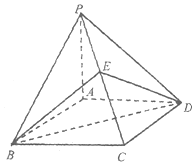 如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.(I)求证:PA∥平面BED
( II)求二面角C-BE-D的余弦值.
分析 (I)连结AC,设BD与AC交于点D,连结OE,证明OE∥PA,即可证明PA∥平面BED
( II)过O作OF⊥BE,垂足为F,连CF,由三垂线定理,得CF⊥BE,故∠OFC为二面角C-BE-D的平面角,在Rt△COF中,求二面角C-BE-D的余弦值.
解答  (I)证明:连结AC,设BD与AC交于点D,连结OE.
(I)证明:连结AC,设BD与AC交于点D,连结OE.
∴ABCD是菱形,∴O是AC的中点,
∵点E为PC的中点,∴OE∥PA.
∵OE?平面BFD,PA?平面BFD,…(2分)
∴PA∥平面BED. …(4分)
(II)解:∵PA⊥平面ABCD,AC?平面ABCD,
∴PA⊥AC.
由(I)知OE∥PA,∴OE⊥AC.…(5分)
∵ABCD是菱形,∴AC⊥BD.
∵OE∩BD=O,∴AC⊥平面BED. …(6分)
过O作OF⊥BE,垂足为F,连CF,由三垂线定理,得CF⊥BE,故∠OFC为二面角C-BE-D的平面角.
由∠ABC=60°知△ABC为正三角形,
∵PB和平面ABCD所成的角为∠PBA=45°
∴PA=AB,设PA=AB=a,则$OE=\frac{1}{2}a,BO=\frac{{\sqrt{3}}}{2}a$$,BE=\sqrt{B{O^2}+O{E^2}}=a$.
在Rt△COF中,$OF=\frac{OE•BO}{BE}=\frac{{\sqrt{3}}}{4}a$,$OC=\frac{1}{2}a$,$CF=\sqrt{O{C^2}+O{F^2}}=\frac{{\sqrt{7}}}{4}a$,
∴$cos∠OFC=\frac{OF}{CF}=\frac{{\sqrt{3}}}{{\sqrt{7}}}=\frac{{\sqrt{21}}}{7}$
∴二面角C-BE-D的余弦值是$\frac{\sqrt{21}}{7}$…(12分)
点评 本题考查线面平行,考查二面角C-BE-D的余弦值,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(2)从第(1)问抽取的4位居民中随机抽取2位,恰有1男1女的概率是多少;
(3)由以上数据,能否有99%的把握认为在20:00-22:00时间段的休闲方式与性别有关系.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | a1,a2,a3成等比数列 | B. | a2,a3,a6成等比数列 | ||
| C. | a3,a4,a8成等比数列 | D. | a4,a6,a9成等比数列 |
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{4\sqrt{6}}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{7}$ | D. | $\frac{6}{5}$ |