Question

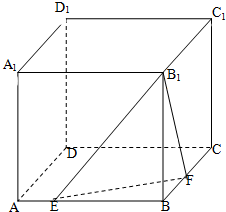棱长为m的正方体ABCD-A₁B₁C₁D₁，E、F分别是棱AB，BC上的动点，且AE=BF．
（1）求异面直线A₁F与C₁E所成角；
（2）当三棱锥B₁-BEF的体积取得最大时，求二面角B₁-EF-B的余弦值．

Answer 1

考点：用空间向量求平面间的夹角,异面直线及其所成的角

专题：空间角

分析：（1）以D为原点，DA，DC，DD₁分别为x，y，z轴建立空间直角坐标系，设AE=BF=x，求出相关点的坐标，通过计算

A1F

•

C1E

=0，说明A₁F与C₁E所成角为

π

2

．
（2）求出VB1-BEF最大，判断E，F分别为AB，BF的中点，求出设平面B₁EF的法向量，平面BEF的法向量，利用向量的数量积求解即可求出二面角B₁-EF-B的余弦值．

解答： 解：（1）以D为原点，DA，DC，DD₁分别为x，y，z轴建立空间直角坐标系
设AE=BF=x，则A₁（m，0，m），F（m-x，m，0），E（m，x，0），C₁（0，m，m），B（m，m，0），B₁（m，m，m）
所以

A1F

=(-x，m，-m)，

C1E

=(m，x-m，-m)…（4分）．
则

A1F

•

C1E

=-mx+m(x-m)+m2=0
所以A₁F与C₁E所成角为

π

2

…（6分）
（2）因为VB1-BEF=

1

3

(

1

2

BE•BF)B1B
又因为BE=m-x，BF=x，B₁B=m，
VB1-BEF=

1

6

m(-x2+mx)
当x=

m

2

时，VB1-BEF最大
所以E，F分别为AB，BF的中点
所以E(m，

m

2

，0)，F(

m

2

，m，0)
所以

FB1

=(

m

2

，0，m)，

EB1

=(0，

m

2

，m)…（8分）
设平面B₁EF的法向量为

n

=(x，y，z)
由

EB 1 • n =0 FB1 • n =0

得

n

=(-2，-2，1)
平面BEF的法向量为

BB1

=(0，0，1)，
cos＜

n

•

BB1

＞=

n • BB1

| n • BB1 |

=

1

3

．
所以二面角B₁-EF-B的余弦值为

1

3

…（12分）

点评：本题考查空间向量求解二面角的平面角的余弦值，空间向量求解异面直线所成角的方法，考查转化思想以及计算能力．