题目内容
已知函数f(x)=2cos(
x-
)
(1)求f(x)的最小正周期及单调递减区间;
(2)若α∈[-
,
],且f(2α)=1,求α的值;
(3)若x∈[0,
],求函数f(x)的值域.
| 1 |
| 2 |
| π |
| 6 |
(1)求f(x)的最小正周期及单调递减区间;
(2)若α∈[-
| π |
| 2 |
| π |
| 2 |
(3)若x∈[0,
| π |
| 2 |
考点:三角函数的周期性及其求法,余弦函数的单调性
专题:三角函数的图像与性质
分析:(1)根据三角函数的性质即可求f(x)的最小正周期及单调递减区间;
(2)根据f(2α)=1,解方程即可,求α的值;
(3)根据函数的性质即可求函数f(x)的值域.
(2)根据f(2α)=1,解方程即可,求α的值;
(3)根据函数的性质即可求函数f(x)的值域.
解答:
解:(1)f(x)的最小正周期T=
=4π,
由2kπ≤
x-
≤2kπ+π,k∈Z,
解得4kπ+
≤x≤4kπ+
,k∈Z,
即函数的单调递减区间为[4kπ+
,kπ+
],k∈Z;
(2)由f(2α)=2cos(α-
)=1,
得cos(α-
)=
,
若α∈[-
,
],则α-
∈[-
,
],
则α=-
或
;
(3)若x∈[0,
],则
x-
∈[-
,
],
则cos(
x-
)∈[
,1],
即函数f(x)∈[
,2],
则函数f(x)的值域为[
,2].
| 2π | ||
|
由2kπ≤
| 1 |
| 2 |
| π |
| 6 |
解得4kπ+
| π |
| 3 |
| 7π |
| 3 |
即函数的单调递减区间为[4kπ+
| π |
| 3 |
| 7π |
| 3 |
(2)由f(2α)=2cos(α-
| π |
| 6 |
得cos(α-
| π |
| 6 |
| 1 |
| 2 |
若α∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
则α=-
| π |
| 6 |
| π |
| 2 |
(3)若x∈[0,
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
则cos(
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
即函数f(x)∈[
| 3 |
则函数f(x)的值域为[
| 3 |
点评:本题主要考查三角函数的周期性,单调性和值域的求解,综合考查三角函数的图象和性质.

练习册系列答案
相关题目
已知向量
,
满足|
|=2,
与
的夹角为60°,则
在
上的投影是( )
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-1 |
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+3x+b(b为常数),则f(-1)=( )
| A、5 | B、6 | C、-6 | D、-5 |
已知函数f(x),g(x)分别是定义在R上的奇函数与偶函数,且f(x)=g(x-1),则g(2015)=( )
| A、0 | B、1 |
| C、2014 | D、2015 |
若函数y=f(x)的定义域是[-1,1],则函数g(x)=
的定义域是( )
| f(x2) |
| x-1 |
| A、[-1,1) |
| B、[0,1) |
| C、[-1,0)∪(0,1) |
| D、[-1,1] |
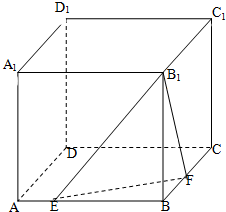 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.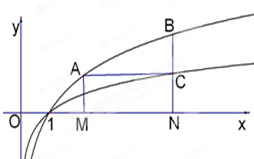 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.