题目内容
求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.




考点:棱柱、棱锥、棱台的体积,旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:画出几何体的图形,求出圆台的上下底的半径,求出母线长,即可求解表面积以及体积.
解答:
解:如图,设圆台上,下底面半径是r1,r2,过C点作CF⊥AB,由∠ADC=135°,CE⊥AD,CD=2
得∠EDC=45°,r1=CE=2,

则CF=4,BF=3,CF⊥AB,得BC=5,r2=AB=5,
∴S表面=S下底面+S台侧面+S锥侧面
=π×r22+π×(r2+r1)×5+π×r1×CD
=π×52+π×(2+5)×5+π×2×2
=(60+4
)π.
V=V台-V锥
=
π(
+r1r2+
)AE-
π
DE
=
π(
+2×5+
)4-
π
×2
=
π.
| 2 |

则CF=4,BF=3,CF⊥AB,得BC=5,r2=AB=5,
∴S表面=S下底面+S台侧面+S锥侧面
=π×r22+π×(r2+r1)×5+π×r1×CD
=π×52+π×(2+5)×5+π×2×2
| 2 |
=(60+4
| 2 |
V=V台-V锥
=
| 1 |
| 3 |
| r | 2 1 |
| r | 2 2 |
| 1 |
| 3 |
| r | 2 1 |
=
| 1 |
| 3 |
| 2 | 2 |
| 5 | 2 |
| 1 |
| 3 |
| 2 | 2 |
=
| 148 |
| 3 |
点评:本题考查旋转体的应用,考查空间想象能力以及计算能力,求出相关的数值,判断几何体的图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
已知a,b均为正数,
+
=1,则使a+b≥c恒成立的实数c的取值范围是( )
| 1 |
| a |
| 4 |
| b |
| A、c≤9 | B、c≥9 |
| C、c≤10 | D、c≥10 |
若平面向量
与
=(1,-2)的夹角是180°,且|
|=3
,则
等于( )
| a |
| b |
| a |
| 5 |
| a |
| A、.(6,-3) |
| B、(3,-6) |
| C、(-3,6) |
| D、(-6,3) |
已知向量
,
满足|
|=2,
与
的夹角为60°,则
在
上的投影是( )
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-1 |
已知函数f(x),g(x)分别是定义在R上的奇函数与偶函数,且f(x)=g(x-1),则g(2015)=( )
| A、0 | B、1 |
| C、2014 | D、2015 |
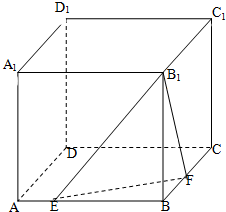 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.