题目内容
10.已知函数$f(x)=\sqrt{3}sin({ωx+ω})-cos({ωx+ω})({-\frac{π}{2}<φ<0,ω>0})$为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为$\frac{π}{2}$.(1)求$f({\frac{π}{24}})$的值;
(2)将y=f(x)的图象向右平移$\frac{π}{6}$个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在$[{-\frac{π}{3},\frac{5π}{6}}]$上的最值.
分析 (1)通过两角差的正弦函数化简函数的表达式,求出函数的周期,利用函数是偶函数求出φ,然后求解$f({\frac{π}{24}})$的值.
(2)由函数图象的变换可求g(x)=-2cos($\frac{1}{2}$x-$\frac{π}{3}$),利用余弦函数的单调性可求y=g(x)的单调区间,由x∈$[{-\frac{π}{3},\frac{5π}{6}}]$,结合函数的单调性可求最大值.
解答 (本题满分为12分)
解:(1)函数f(x)=$\sqrt{3}$sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-$\frac{π}{6}$),…1分
因为函数是偶函数,
所以φ-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得:φ=kπ+$\frac{2π}{3}$,k∈Z,
∵-$\frac{π}{2}$<φ<0,
∴φ=-$\frac{π}{3}$.
函数y=f(x)图象的两相邻对称轴间的距离为$\frac{π}{2}$,
所以T=π,T=$\frac{2π}{ω}$=π,所以ω=2;
f(x)=2sin(2x-$\frac{π}{2}$)=-2cos2x,…5分
则f($\frac{π}{24}$)=-2cos(2×$\frac{π}{24}$)=-2cos($\frac{π}{3}$-$\frac{π}{4}$)=-$\frac{\sqrt{6}+\sqrt{2}}{2}$,…6分
(2)由函数图象的变换可知,y=g(x)=-2cos($\frac{1}{2}$x-$\frac{π}{3}$),…8分
由2kπ≤$\frac{1}{2}$x-$\frac{π}{3}$≤2kπ+π,k∈Z,解得:4kπ+$\frac{2π}{3}$≤x≤4kπ+$\frac{8π}{3}$,k∈Z,
即函数y=g(x)的单调递增区间为:[4kπ+$\frac{2π}{3}$,4kπ+$\frac{8π}{3}$]k∈Z,
由2kπ+π≤$\frac{1}{2}$x-$\frac{π}{3}$≤2kπ+2π,k∈Z,解得:4kπ+$\frac{8π}{3}$≤x≤4kπ+$\frac{14π}{3}$,k∈Z,
即函数y=g(x)的单调递减区间为:[4kπ+$\frac{8π}{3}$,4kπ+$\frac{14π}{3}$]k∈Z,…10分
∵x∈$[{-\frac{π}{3},\frac{5π}{6}}]$,
∴结合函数的单调性可知:
当$\frac{1}{2}$x-$\frac{π}{3}$=0,即x=$\frac{2π}{3}$时,y=g(x)最小值为-2…11分
当$\frac{1}{2}$x-$\frac{π}{3}$=-$\frac{π}{2}$,即x=-$\frac{π}{3}$时,y=g(x)最大值为0…12分
点评 本题主要考查了两角差的正弦函数公式,周期公式,三角函数图象的变换规律,余弦函数的单调性,考查了数形结合思想和转化思想的应用,属于中档题.

 如图是某个几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体外接球的直径为( )
如图是某个几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体外接球的直径为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
| A. | $-\frac{5}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $-\frac{5}{2}$ | D. | $-\frac{1}{2}$ |
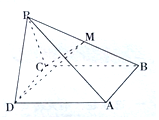 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°. 某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.
某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.