题目内容
15.已知命题p:方程$\frac{x^2}{m+1}+\frac{y^2}{3-m}=1$表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.分析 若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,进而可得实数m的取值范围.
解答 解:∵方程$\frac{x^2}{m+1}+\frac{y^2}{3-m}=1$表示焦点在y轴上的椭圆,
∴0<m+1<3-m,
解得:-1<m<1,
∴若命题p为真命题,求实数m的取值范围是(-1,1);
若关于x的方程x2+2mx+2m+3=0无实根,则判别式△=4m2-4(2m+3)<0,
即m2-2m-3<0,得-1<m<3.
若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,
若p真q假,则$\left\{\begin{array}{l}-1<m<1\\ m≥3,或m≤-1\end{array}\right.$,此时无解,
柔p假q真,则$\left\{\begin{array}{l}-1<m<3\\ m≥1,或m≤-1\end{array}\right.$,得1≤m<3.
综上,实数m的取值范围是[1,3).
点评 本题以命题的真假判断与应用为载体,考查了椭圆的标准方程,方程根的存在性及个数判断,难度中档.

练习册系列答案
相关题目
6.“a≠1或b≠2”是“a+b≠3”的( )
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
3.设f(x)是定义在R上的奇函数,其图象关于直线x=1对称,且当0<x≤1时,f(x)=log3x.记f(x)在[-10,10]上零点的个数为m,方程f(x)=-1在[-10,10]上的实数根和为n,则有( )
| A. | m=20,n=10 | B. | m=10,n=20 | C. | m=21,n=10 | D. | m=11,n=21 |
5.某几何体的三视图如图所示,则该几何体的表面积为( )
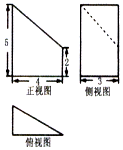

| A. | 45 | B. | $45+\frac{{9\sqrt{2}}}{2}$ | C. | $\frac{117}{2}$ | D. | 60 |